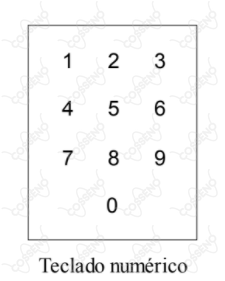
O sistema de segurança de uma casa utiliza um teclado numérico, conforme ilustrado na figura. Um ladrão observa de longe e percebe que:
• a senha utilizada possui dígitos;
• o primeiro e o último dígitos encontram-se numa mesma linha;
• o segundo e o terceiro dígitos encontram-se na linha imediatamente superior.
Calcule o número de senhas que deverão ser experimentadas pelo ladrão para que com certeza ele consiga entrar na casa.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, a ideia central é interpretar como a segunda e a terceira preposição se comportam mutuamente. No caso, iremos trabalhar com duas linhas subsequentes; uma primeira para os dígitos dos extremos, e uma segunda para os dígitos intermediários. Ou seja, a primeira linha não pode ser a $(1,2,3)$, visto que não há linha imediatamente acima, logo, só existem três opções para primeira linha. No entanto, essas três opções não apresentam a mesma generalidade; a linha que apresenta só o $0$ é um problema, pois escolher ela para primeira linha imputa os dígitos dos extremos serem ambos iguais a $0$. Nesse contexto, a ideia é dividir em casos, são eles:
$• \ \text{Caso I:}$ $\color{#3368b8}{\text{A primeira linha não é a do 0}}$
Para este caso, existem duas opções para primeira linha, ela pode ser a $(7,8,9)$ ou a $(4,5,6)$, independe qual for, os dígitos do extremos apresentam $3$ opções cada:\begin{matrix}
\underset{\_\_\_}{\color{orangered}{3}} & \underset{\_\_\_}{?} & \underset{\_\_\_}{?} & \underset{\_\_\_}{\color{orangered}{3}}
\end{matrix}Veja que para qualquer uma das duas opções a segunda linha (subsequente) é análoga, ou seja, qualquer uma delas apresentam $3$ opções para os dígitos intermediários.\begin{matrix}
\underset{\_\_\_}{\color{orangered}{3}} & \underset{\_\_\_}{\color{#3368b8}{3}} &\underset{\_\_\_}{\color{#3368b8}{3}} & \underset{\_\_\_}{\color{orangered}{3}}
\end{matrix}Agora, conforme o princípio multiplicativo, dada as duas opções possíveis para cada caso:\begin{matrix}
2 \cdot (3\cdot 3 \cdot 3\cdot 3) = 162
\end{matrix}$• \ \text{Caso II:}$ $\color{#3368b8}{\text{A primeira linha é a do 0}}$
Neste caso, o primeiro e o último dígito já estão definidos; ambos são iguais a $0$. Como resultado, segue o raciocínio anterior para a segunda linha, esta que deve ser obrigatoriamente a $(7,8,9)$:\begin{matrix}
\underset{\_\_\_}{\color{orangered}{1}} & \underset{\_\_\_}{\color{#3368b8}{3}} &\underset{\_\_\_}{\color{#3368b8}{3}} & \underset{\_\_\_}{\color{orangered}{1}}
\end{matrix}Novamente, conforme princípio multiplicativo:\begin{matrix}
1 \cdot ( 1\cdot 3 \cdot 3\cdot 1) = 9
\end{matrix}Portanto, o número total de senhas possíveis são:\begin{matrix}162+ 9
= 171 \ \text{senhas} & \tiny{\blacksquare}
\end{matrix}

20:44 11/04/2024
171, o código penal que o ladrão vai receber quando entrar na casa kkkkkkkkk

