Um pequeno bloco pesando está preso por uma corda em um plano inclinado, como mostra a figura. No instante , a corda se rompe. Em , o bloco atinge o líquido e submerge instantaneamente. Sabendo que o empuxo sobre o bloco é de , e que o coeficiente de atrito dinâmico entre o bloco e a parte emersa do plano inclinado é , determine a distância percorrida pelo bloco a partir do instante inicial até .
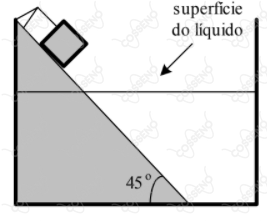
Aceleração da gravidade $g = 10 \ m/s^{2}$.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Antes de entrar no líquido, o corpo se move como uma partícula descendo um plano inclinado com atrito. Assim, orientando o eixo $x$ na direção tangencial ao movimento e o eixo $y$ na direção normal do deslizamento, o diagrama de forças do movimento é apresentado na figura abaixo, à esquerda.
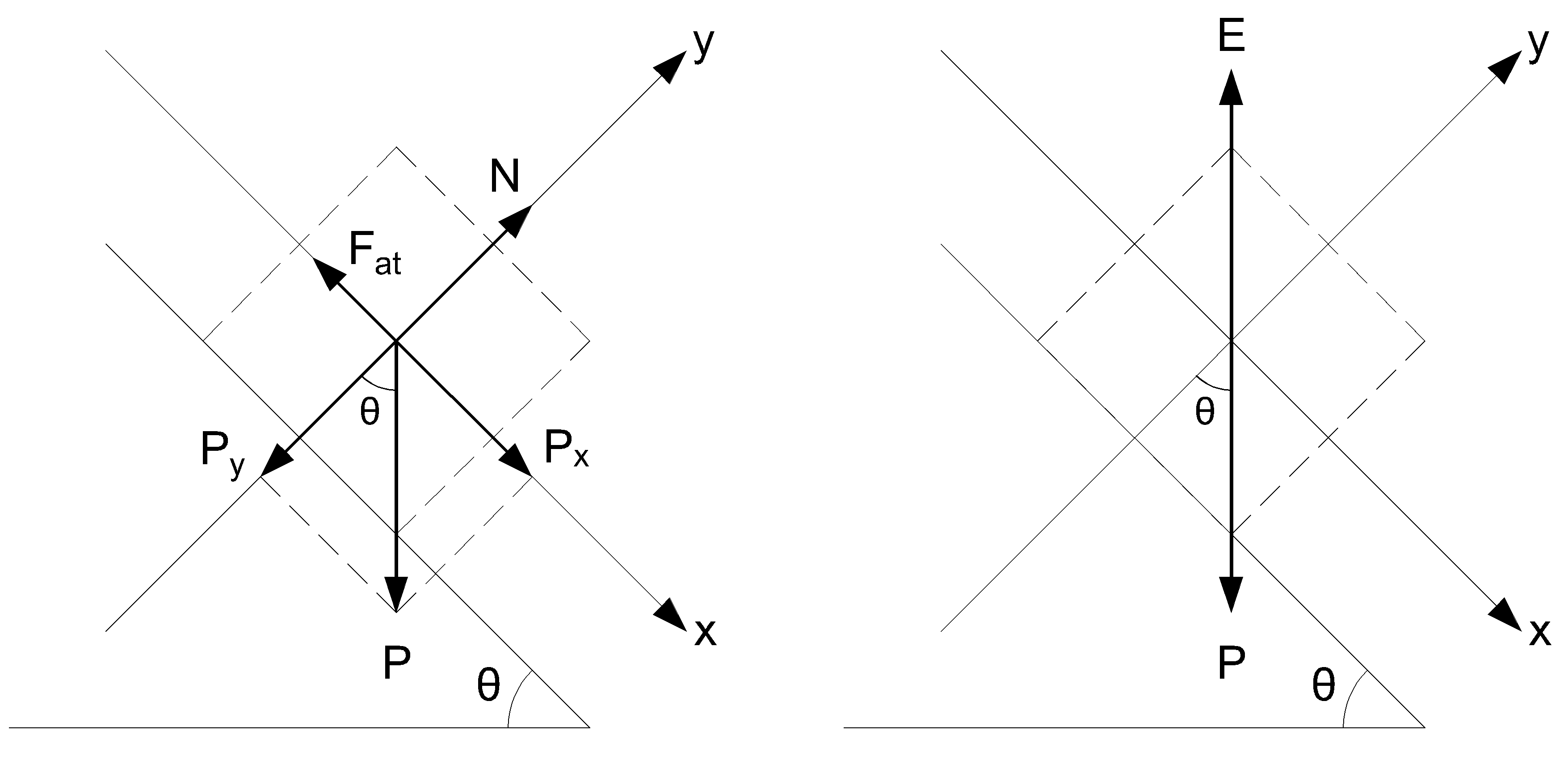 O bloco possui equilíbrio em $y$, logo
$$N=P_y=mg\cos\theta$$
Já em $x$, a resultante $F_r$ das forças é
$$F_r=P_x-F_at=mg\sin\theta-\mu_cN\Rightarrow ma=mg\sin\theta-\mu_cmg\cos\theta$$
$$\Rightarrow a=g(\sin\theta-\mu_c\cos\theta)=10\cdot\left(\frac{\sqrt2}{2}-\frac{0,4\sqrt2}{2}\right)\Rightarrow a=3\sqrt2m/s^2$$
Por todo o intervalo de tempo em que o corpo se desloca no plano até a submersão, ele segue neste movimento de aceleração constante, que é dado pela seguinte equação horária:
$$s=s_0+v_0t+\frac{1}{2}at^2$$
Se o corpo sai do repouso e da origem do sistema de coordenadas, para $t=1$, o deslocamento em $x$ é dado por
$$x_0=\frac{1}{2}at^2=\frac{1}{2}\cdot3\sqrt2\Rightarrow x_0=\frac{3}{2}\sqrt2m$$
Quando o corpo já está submerso, pode-se considerar que as forças de contato com o plano são iminentemente perdidas, e apenas o peso e o empuxo são forças atuantes no corpo (à direita, na imagem). Cabe salientar que o empuxo é uma força normal, mas com relação a superfície do fluido no qual o corpo está imerso, portanto aponta no sentido contrário do peso. Como ambas as forças possuem mesmo módulo, $50N$, elas se anulam. Dessa forma, quando imerso, o corpo apresenta aceleração nula, mas com velocidade adquirida do deslizamento no plano inclinado dada por
$$\Delta v=at\Rightarrow \Delta v=3\sqrt2m/s$$
Mas $\Delta v$ é a própria velocidade $v$ do movimento uniforme subsequente à imersão no fluido. Assim,
$$x=x_0+vt$$
$$x=\frac{3\sqrt2}{2}+3\sqrt2t$$
Nota-se que a equação acima fornece uma expressão para o movimento desde sua origem no espaço, mas não no tempo. Dessa forma,
$$\boxed{x(t)=\frac{3\sqrt2}{2}+3\sqrt2(t-1)}$$
$$x=\frac{3\sqrt2}{2}+3\sqrt2(3-1)$$
$$\boxed{x=\frac{15\sqrt2}{2}m}$$
O bloco possui equilíbrio em $y$, logo
$$N=P_y=mg\cos\theta$$
Já em $x$, a resultante $F_r$ das forças é
$$F_r=P_x-F_at=mg\sin\theta-\mu_cN\Rightarrow ma=mg\sin\theta-\mu_cmg\cos\theta$$
$$\Rightarrow a=g(\sin\theta-\mu_c\cos\theta)=10\cdot\left(\frac{\sqrt2}{2}-\frac{0,4\sqrt2}{2}\right)\Rightarrow a=3\sqrt2m/s^2$$
Por todo o intervalo de tempo em que o corpo se desloca no plano até a submersão, ele segue neste movimento de aceleração constante, que é dado pela seguinte equação horária:
$$s=s_0+v_0t+\frac{1}{2}at^2$$
Se o corpo sai do repouso e da origem do sistema de coordenadas, para $t=1$, o deslocamento em $x$ é dado por
$$x_0=\frac{1}{2}at^2=\frac{1}{2}\cdot3\sqrt2\Rightarrow x_0=\frac{3}{2}\sqrt2m$$
Quando o corpo já está submerso, pode-se considerar que as forças de contato com o plano são iminentemente perdidas, e apenas o peso e o empuxo são forças atuantes no corpo (à direita, na imagem). Cabe salientar que o empuxo é uma força normal, mas com relação a superfície do fluido no qual o corpo está imerso, portanto aponta no sentido contrário do peso. Como ambas as forças possuem mesmo módulo, $50N$, elas se anulam. Dessa forma, quando imerso, o corpo apresenta aceleração nula, mas com velocidade adquirida do deslizamento no plano inclinado dada por
$$\Delta v=at\Rightarrow \Delta v=3\sqrt2m/s$$
Mas $\Delta v$ é a própria velocidade $v$ do movimento uniforme subsequente à imersão no fluido. Assim,
$$x=x_0+vt$$
$$x=\frac{3\sqrt2}{2}+3\sqrt2t$$
Nota-se que a equação acima fornece uma expressão para o movimento desde sua origem no espaço, mas não no tempo. Dessa forma,
$$\boxed{x(t)=\frac{3\sqrt2}{2}+3\sqrt2(t-1)}$$
$$x=\frac{3\sqrt2}{2}+3\sqrt2(3-1)$$
$$\boxed{x=\frac{15\sqrt2}{2}m}$$

Ampliar Imagem

