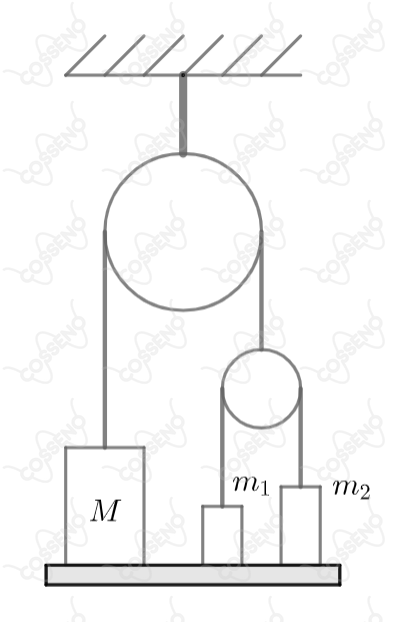
Sejam , e as massas dos blocos homogêneos dispostos conforme a figura ao lado, inicialmente apoiados sobre uma placa horizontal. Determine a aceleração do bloco de massa , em relação a roldana fixa, após a retirada da placa, sabendo que e . Considere que não há atrito no sistema e despreze o peso das polias e das cordas que unem os blocos.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Seja $a_{1}$ a aceleração do bloco $m_{1}$, $a_{2}$ a aceleração do bloco $m_{2}$ e $a_{3}$ a aceleração do bloco $M$. Utilizando vínculos geométricos, podemos encontrar que
$$2a_{3} = a_{1} + a_{2}.$$ Sabendo disso, basta utilizar as leis de Newton em cada bloco.
$$Mg - 2T = Ma_{3} \\
T - m_{1}g = m_{1}a_{1}\\
m_{2}g - T = m_{2}a_{2}. $$ Com isso, basta isolar as acelerações de cada equação acima e substituir na equação dos vínculos a fim de encontrar a tração $T$. Fazendo um pouco de manipulação algébrica chegamos em
$$T = \dfrac{4m_{1}m_{2}M}{4m_{1}m_{2} + m_{1}M + m_{2}M}g.$$ Agora basta retornar na equação do bloco $m_{1}$ e encontrar a aceleração $a_{1}$.
$$a_{1} = \dfrac{M^{2} - 4m_{2}^{2}}{M^{2} + 4m_{1}m_{2}}g.$$

