Inicialmente, temos: $$\begin{cases}P_1=\pu{2 atm}\\ V_1=\pu{3\cdot 10^{-3} m3}\\ T_1=\pu{300 K}\end{cases}$$ Após o primeiro processo, teremos $T_2=\pu{500 K}$ e: $$V_2=\dfrac{T_2}{T_1}V_1=5\cdot 10^{-3}\text{ m}^3$$ Após o segundo processo, teremos $T_3=\pu{250 K}$ e: $$P_3=\dfrac{T_3}{T_2}P_2=1\cdot 10^{5}\text{ Pa}$$ Como estamos lidando com um ciclo termodiâmico, já podemos determinar os valores de pressão e temperatura a ligando os pontos no diagrama PV, dado que o processo 3 é isobárico e o 4 é isocórico. 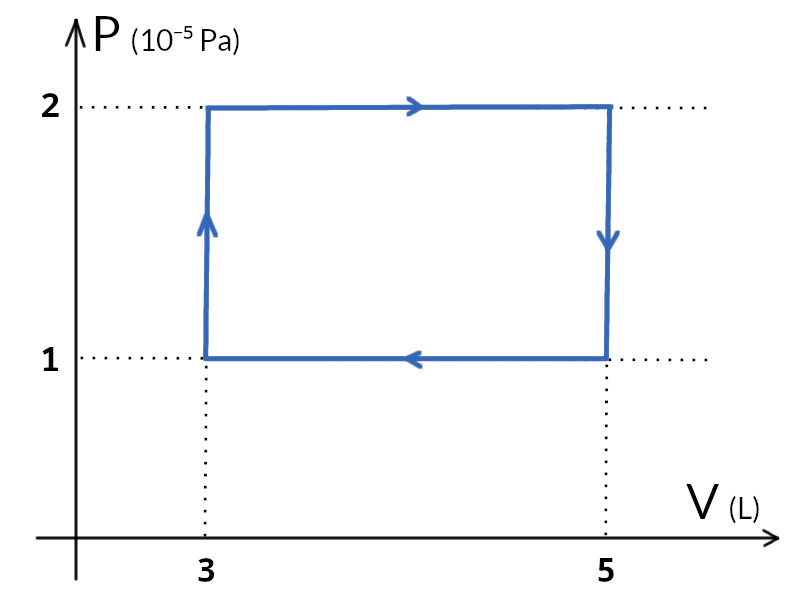Assim, para calcular o trabalho basta calcular a área do retângulo acima: $$\begin{align*}&W=1\cdot 10^5\cdot 2\cdot 10^{-3}\\ &\boxed{W=\pu{200 J}}\end{align*}$$ Enquanto o calor líquido produzido ao longo do ciclo pode ser determinado pela primeira lei da termodinâmica: $$Q=\Delta U + W$$ Como estamos lidando com um ciclo, o estado final é igual ao inicial, e assim $\Delta U = 0$, fazendo com que o calor líquido também seja $Q=W=\pu{200 J}$.