Deslocando-se em uma pista retilínea horizontal, os dois carrinhos de madeira e , representados na figura abaixo, colidem frontalmente, sendo o coeficiente de restituição do choque. Sobre a face posterior do carrinho está fixada uma placa metálica , que, no instante do choque, dista de uma placa metálica idêntica , fixada no ponto .
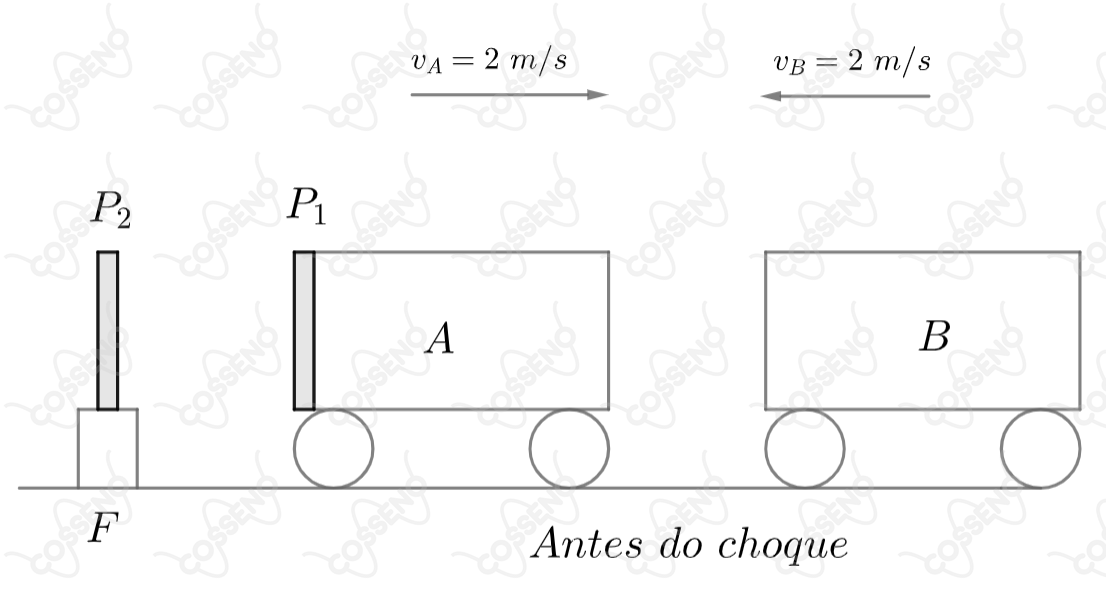

Sabendo-se que entre as duas placas existe uma capacitância de e uma tensão de , determine: a carga elétrica, a capacitância e a tensão elétrica entre as placas após o choque.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$-$ A priori, do impacto, têm-se:
\begin{matrix} e = \large{ \frac{|V_f|}{|V_i|}} = \frac{x+1,2}{2+2} &\Rightarrow& \fbox{$x = 2 \ m$}
\end{matrix} Logo, a distância percorrida em $0,5 \ s$ \begin{matrix} \Delta S = x \ . \ t &\Rightarrow& \fbox{$\Delta S = 1 \ m$}
\end{matrix} $-$ Agora, com conhecimento da capacitância e tensão, podemos encontrar a carga elétrica, veja:
\begin{matrix} Q = C_1.\Delta V_1 &\Rightarrow& \fbox{$Q = 96 \ C$}
\end{matrix} $-$ Sabido que, a carga elétrica é a mesma, temos a relação:
\begin{matrix} C_1.\Delta V_1 = C_2.\Delta V_2 & (1)
\end{matrix} Da capacitância, encontramos: \begin{matrix} C = \large{\frac{\epsilon \ .\ A}{S}} &\Rightarrow& \large{\frac{C_2}{C_1} = \frac{S_2}{S_1}} &\Rightarrow& \fbox{$C_2 = 12 \ \mu F$}
\end{matrix} $\color{orangered}{Obs:}$ $S_1 = 3 \ \ \ , \ \ \ S_2 = 3 - \Delta S$
$-$ Voltando da equação $(1)$, substituindo nossos resultado, constatamos que:
\begin{matrix} \fbox{$\Delta V_2 = 8 \ V $}
\end{matrix}


