Entre duas placas metálicas paralelas, e que constituem um capacitor de capacitância , coloca-se esticado um fio de náilon que vibra na frequência fundamental .
Retira-se o fio, altera-se a distância entre as placas e coloca-se entre elas um outro fio de náilon, com as mesmas propriedades físicas do primeiro, porém de comprimento tal que, agora, a frequência fundamental de vibração seja .
Sabendo que as placas permanecem sempre carregadas com , determine a tensão elétrica entre elas na segunda distância da experiência.
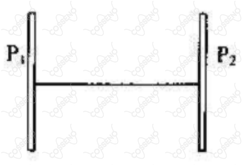
Obs: Não considere o efeito dielétrico do fio de náilon.
$-$ Segundo o enunciado, podemos admitir o meio como homogêneo, vide as propriedades físicas de ambos os fios serem constantes. Dessa forma, com conhecimento que na frequência fundamental temos: $f = \lambda/2$, podemos escrever:
\begin{matrix} v_1 = v_2 &\Rightarrow& \lambda_1 \ . \ f_1 = \lambda_2 \ . \ f_2 &\Rightarrow& \large{\frac{L_1}{L_2} = \frac{f_2}{f_1}}
\end{matrix} $-$ Atente que, a carga $Q$ é constante, então, têm-se a relação:
\begin{matrix} Q = C_1 \ . \ V_1&\Rightarrow& \fbox{$V_1 = 25 \ V$}
\end{matrix} Além disso, \begin{matrix} C_1 \ . \ V_1 = C_2 \ . \ V_2 & (1)
\end{matrix} $-$ Da capacitância, encontramos: \begin{matrix} C = \large{\frac{\epsilon \ .\ A}{L}} &\Rightarrow& \large{\frac{C_2}{C_1} = \frac{L_1}{L_2} = \frac{f_2}{f_1}} &\Rightarrow& \fbox{$C_2 = (0,08 \ .\ 2,5) \ \mu F $}
\end{matrix} $-$ Agora, substituindo nossos resultados em $(1)$, constatamos:
\begin{matrix} \fbox{$V_2 = 10 \ V$}
\end{matrix}
