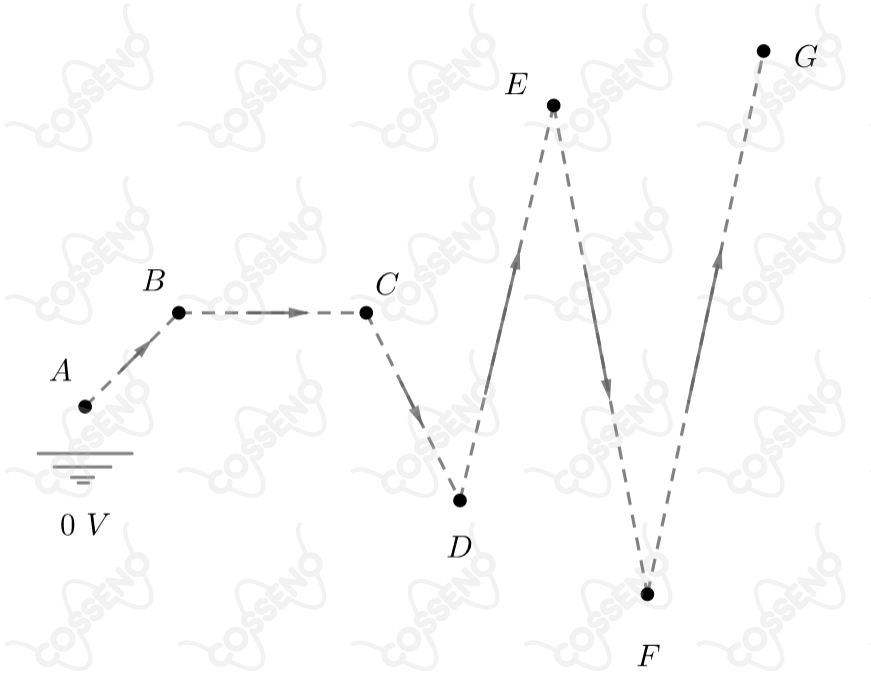
A figura abaixo representa vários pontos imersos num campo elétrico.
Pede-se:
a) Determine o trabalho elétrico necessário para levar uma carga puntiforme de do ponto para o ponto , seguindo o itinerário , mostrado na figura.
b) Determine à energia que seria armazenada num capacitor de se ele fosse ligado entre os pontos e .
DADOS:
Tensões nos pontos:
$V_A=+2\ V\quad V_B=+3\ V\quad V_C=+3\ V\\ V_D=-1\ V\quad V_E=+4\ V\quad V_F=-2\ V\\ V_G=+6\ V$
Tensões nos pontos:
$V_A=+2\ V\quad V_B=+3\ V\quad V_C=+3\ V\\ V_D=-1\ V\quad V_E=+4\ V\quad V_F=-2\ V\\ V_G=+6\ V$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$• \ \text{(a):}$ A força elétrica é conservativa, isto é, o trabalho realizado independe da trajetória, nos importando apenas os pontos inicial e final. Com isso, o trabalho de força elétrica $(W_e)$, temos:
\begin{matrix} W_e =Q.\Delta V &\Rightarrow& W_{AG} = Q . (V_A - V_G ) &\Rightarrow& W_{AG} = -8\ u J
\end{matrix}
$• \ \text{(b):}$ Com conhecimento que a energia armazenada num capacitor é: $E = \frac{C.\Delta V^2}{2} $ , têm-se:
\begin{matrix}E_{CF} = \large{\frac{C.(V_C - V_F)^2}{2}} &\Rightarrow& E_{CF} = \large{\frac{2.[3 - (-2)]^2}{2}} &\Rightarrow& E_{CF} = 25 \ uJ
\end{matrix}

