A princípio, existem algumas formas de resolver este problema, por exemplo; analisar quantas diagonais cortam uma determinada diagonal e assim seguir para todas elas. Todavia, existe uma maneira mais pragmática, veja que o enunciado nos garante que não há mais de que duas diagonais se interceptando no mesmo ponto, ou seja, a cada duas diagonais, têm-se uma única interseção. Nesse sentido, a ideia é pensar em quadriláteros; sabemos que a cada quatro pontos não colineares dois à dois construímos um quadrilátero, e este deve conter duas diagonais, consequentemente, temos uma interseção para cada. (Resumindo, ao selecionarmos quatro pontos, temos uma interseção). Veja um exemplo abaixo: 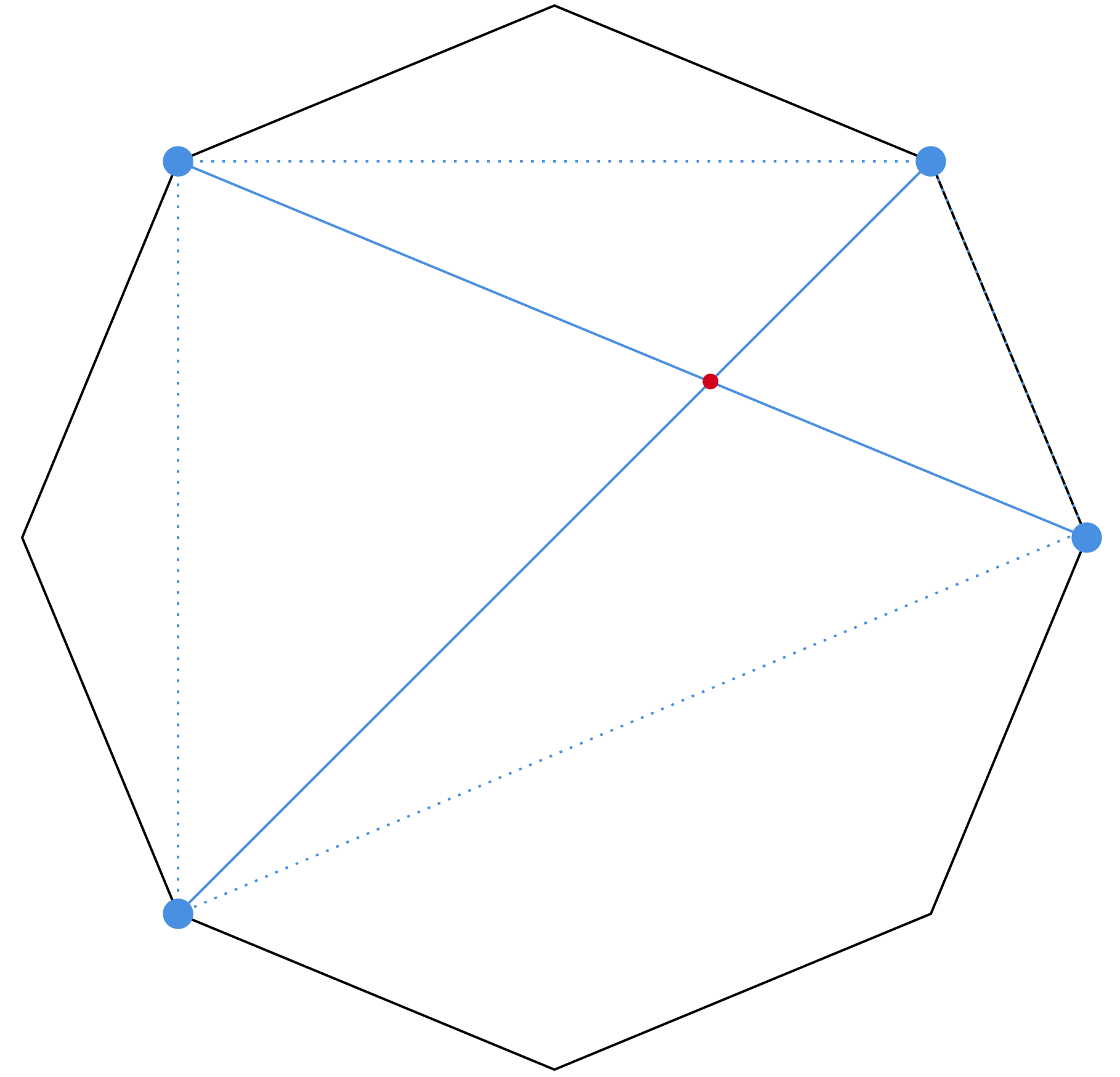Agora, o problema se resume numa combinação, temos oito vértices, e queremos todas as maneiras distintas de selecionar quatro deles, ou seja:\begin{matrix} {\large{{8 \choose 4}}} = \dfrac{8!}{4! \cdot 4!} = 70 \ \text{interseções} & \tiny{\blacksquare} \end{matrix}