Um raio de luz incide sobre a face vertical esquerda de um cubo de vidro de índice de refração , como mostrado na figura.
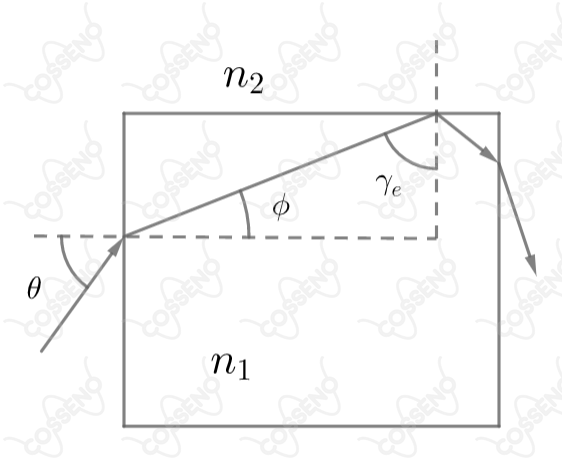
O plano de incidência é o da figura e o cubo está mergulhado em água com índice de refração . Determine o maior ângulo que o raio incidente pode fazer com a face vertical esquerda do cubo para que haja reflexão interna total no topo do cubo.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$-$ A priori, iremos aplicar duas vezes a $\text{Lei de Snell-Descartes}$, começando com o raio incidente no cubo, vejamos:
\begin{matrix} \Large{\frac{\sin{\theta}}{\sin{\phi}}} &=& \Large{\frac{n_1}{n_2}} &\Rightarrow& \cos^2{\gamma} &=& \large{(\frac{n_2}{n_1})^2} & . & \sin^2{\theta}
\end{matrix} $\color{orangered}{Obs:}$ $\color{gray}{\begin{matrix} \phi = 90^{\circ} - \gamma &\Rightarrow& \sin{\phi} = \cos{\gamma} \end{matrix}}$
Agora, para reflexão interna total, temos:
\begin{matrix} \Large{\frac{\sin{\gamma}}{\sin{90^{\circ}}}} &=& \Large{\frac{n_2}{n_1}} &\Rightarrow& \sin^2{\gamma} &=& \large{(\frac{n_2}{n_1})^2}
\end{matrix}
$-$ Com conhecimento da $\text{relação fundamental da trigonometria}$, têm-se:
\begin{matrix} \sin^2{\gamma} + \cos^2{\gamma} = 1 &\Rightarrow& (\frac{n_2}{n_1})^2 + (\frac{n_2}{n_1})^2 \sin^2{\theta} = 1
\end{matrix} Portanto, \begin{matrix}
\theta = \arcsin{\sqrt{(\frac{n_1}{n_2})^2 - 1}}
\end{matrix}

