Considere o veículo de massa percorrendo uma curva inclinada, de ângulo com raio constante, a uma velocidade . Supondo que o coeficiente de atrito dos pneus com o solo seja , calcule as velocidades mínima e máxima com que este veículo pode percorrer esta curva, sem deslizamento.

CossenoGPT
Teste
gratuitamente agora
mesmo! 

Pensando na situação de velocidade máxima e velocidade mínima, pode-se perceber que são duas análises distintas. No caso, para a velocidade máxima, o carro tende a escapar derrapando no sentido de ascender em relação a rampa - o atrito atua contra o sentido do movimento. Por outro lado, para velocidade mínima, o carro tende a descer a rampa, nesse sentido, o atrito atua de forma contrária ao movimento, e em relação a situação anterior. Com isso, vejamos cada caso:
$• \ \text{Velocidade máxima:}$ Decompondo as forças que atuam no carro,
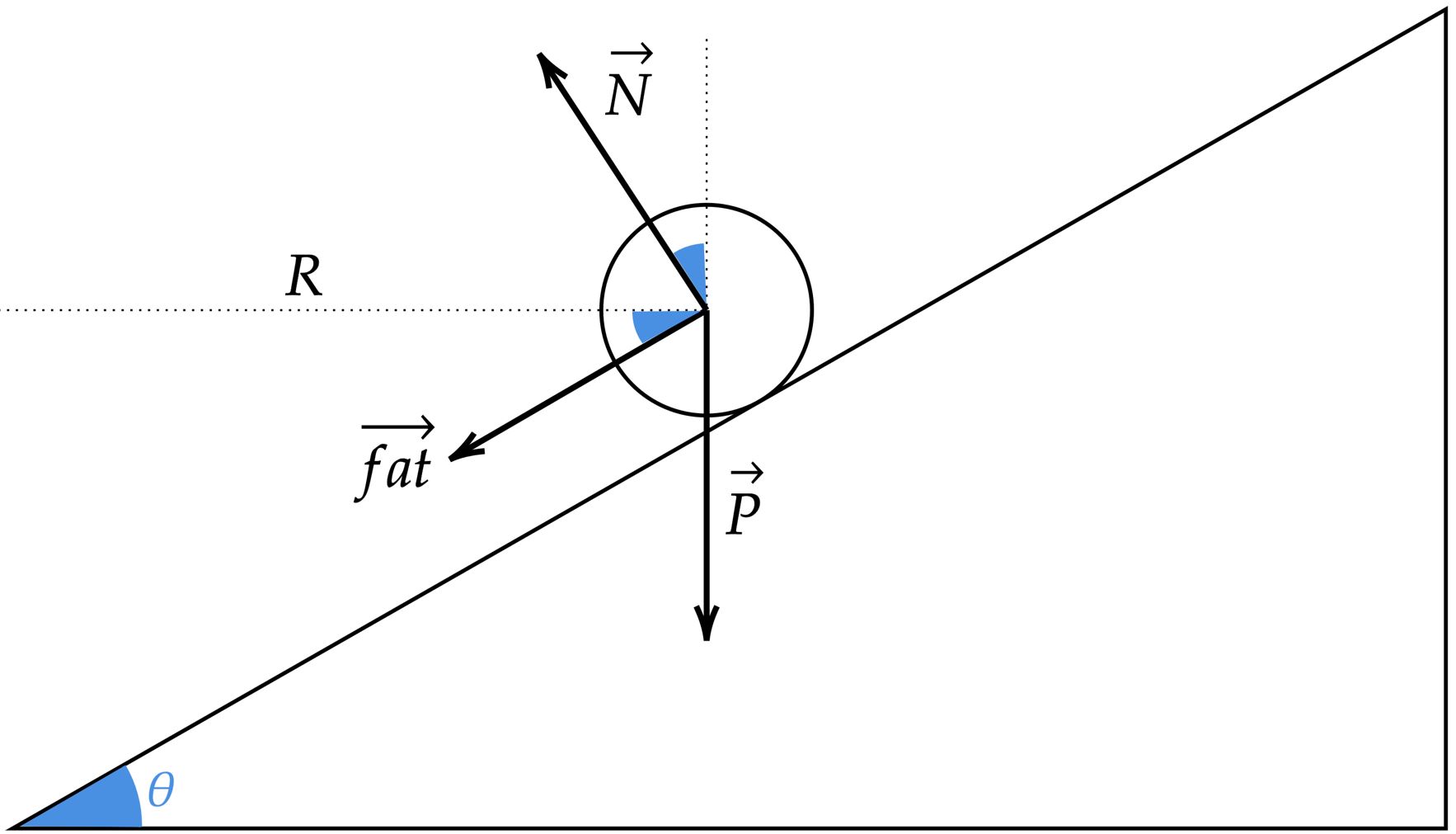 \begin{matrix}
\begin{cases} P&= N \cos{\theta} - (fat)\sin{\theta} \\
R_c &= N \sin{\theta} + (fat)\cos{\theta}
\end{cases} &\Rightarrow & \dfrac{R_c}{P} = \dfrac{\sin{\theta} + \mu \cos{\theta}}{\cos{\theta} - \mu \sin{\theta}} &\therefore &
V_{máx} = \sqrt{Rg \bigg( \dfrac{\sin{\theta} + \mu \cos{\theta}}{\cos{\theta} - \mu \sin{\theta}} \bigg )}
\end{matrix}
$• \ \text{Velocidade mínima:}$ Decompondo as forças que atuam no carro,
\begin{matrix}
\begin{cases} P&= N \cos{\theta} - (fat)\sin{\theta} \\
R_c &= N \sin{\theta} + (fat)\cos{\theta}
\end{cases} &\Rightarrow & \dfrac{R_c}{P} = \dfrac{\sin{\theta} + \mu \cos{\theta}}{\cos{\theta} - \mu \sin{\theta}} &\therefore &
V_{máx} = \sqrt{Rg \bigg( \dfrac{\sin{\theta} + \mu \cos{\theta}}{\cos{\theta} - \mu \sin{\theta}} \bigg )}
\end{matrix}
$• \ \text{Velocidade mínima:}$ Decompondo as forças que atuam no carro,
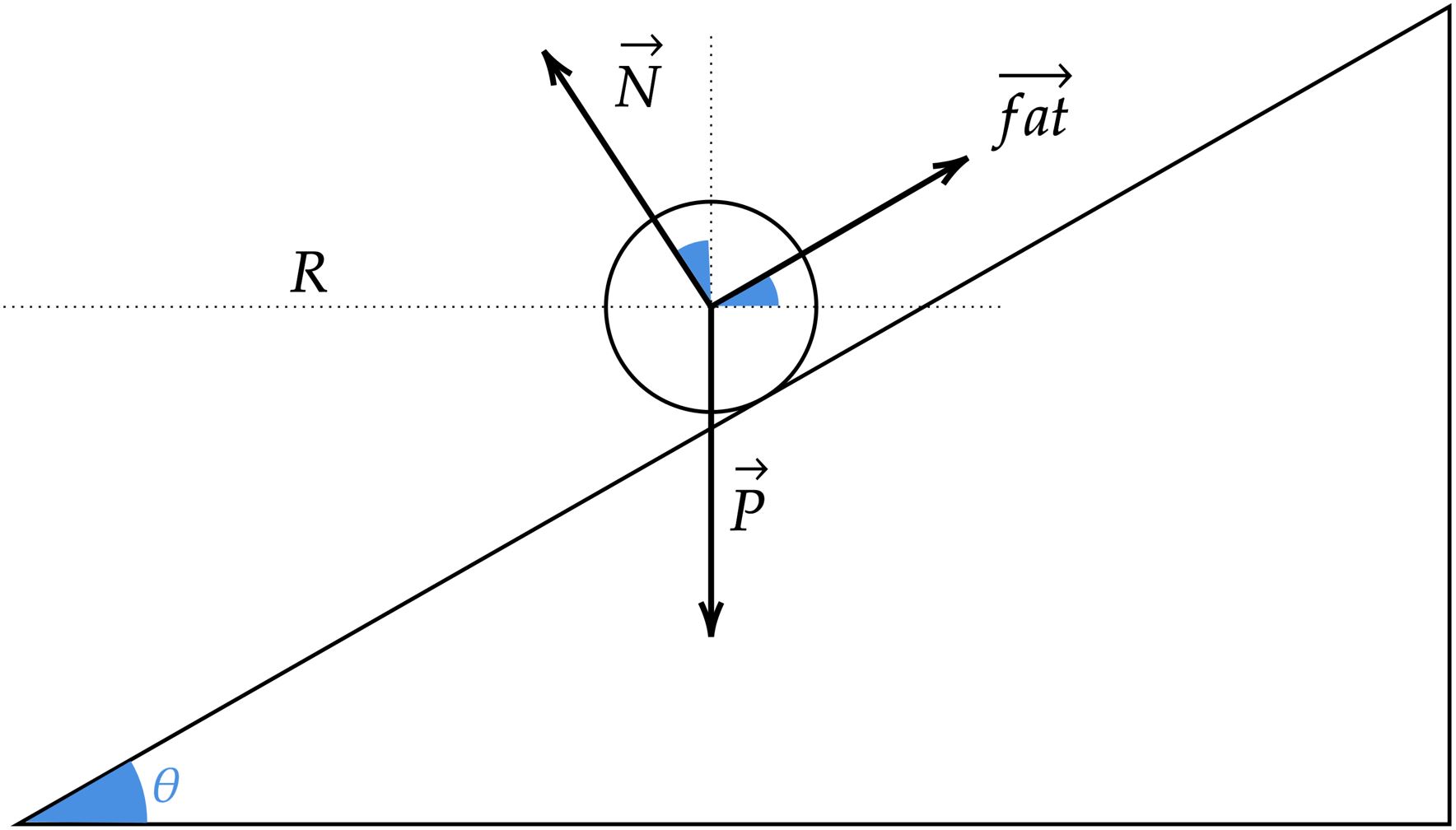 \begin{matrix}
\begin{cases} P&= N \cos{\theta} + (fat)\sin{\theta} \\
R_c &= N \sin{\theta} - (fat)\cos{\theta}
\end{cases} &\Rightarrow & \dfrac{R_c}{P} = \dfrac{\sin{\theta} - \mu \cos{\theta}}{\cos{\theta} + \mu \sin{\theta}} &\therefore &
V_{mín} = \sqrt{Rg \bigg( \dfrac{\sin{\theta} - \mu \cos{\theta}}{\cos{\theta} + \mu \sin{\theta}} \bigg )}
\end{matrix}
\begin{matrix}
\begin{cases} P&= N \cos{\theta} + (fat)\sin{\theta} \\
R_c &= N \sin{\theta} - (fat)\cos{\theta}
\end{cases} &\Rightarrow & \dfrac{R_c}{P} = \dfrac{\sin{\theta} - \mu \cos{\theta}}{\cos{\theta} + \mu \sin{\theta}} &\therefore &
V_{mín} = \sqrt{Rg \bigg( \dfrac{\sin{\theta} - \mu \cos{\theta}}{\cos{\theta} + \mu \sin{\theta}} \bigg )}
\end{matrix}

Ampliar Imagem

Ampliar Imagem

