$• \ \text{Alternativa (a):}$ \begin{matrix} z = i.(1+i) = -1 + i&\Rightarrow& z = (-1,1) \end{matrix} Utilizando do plano complexo: 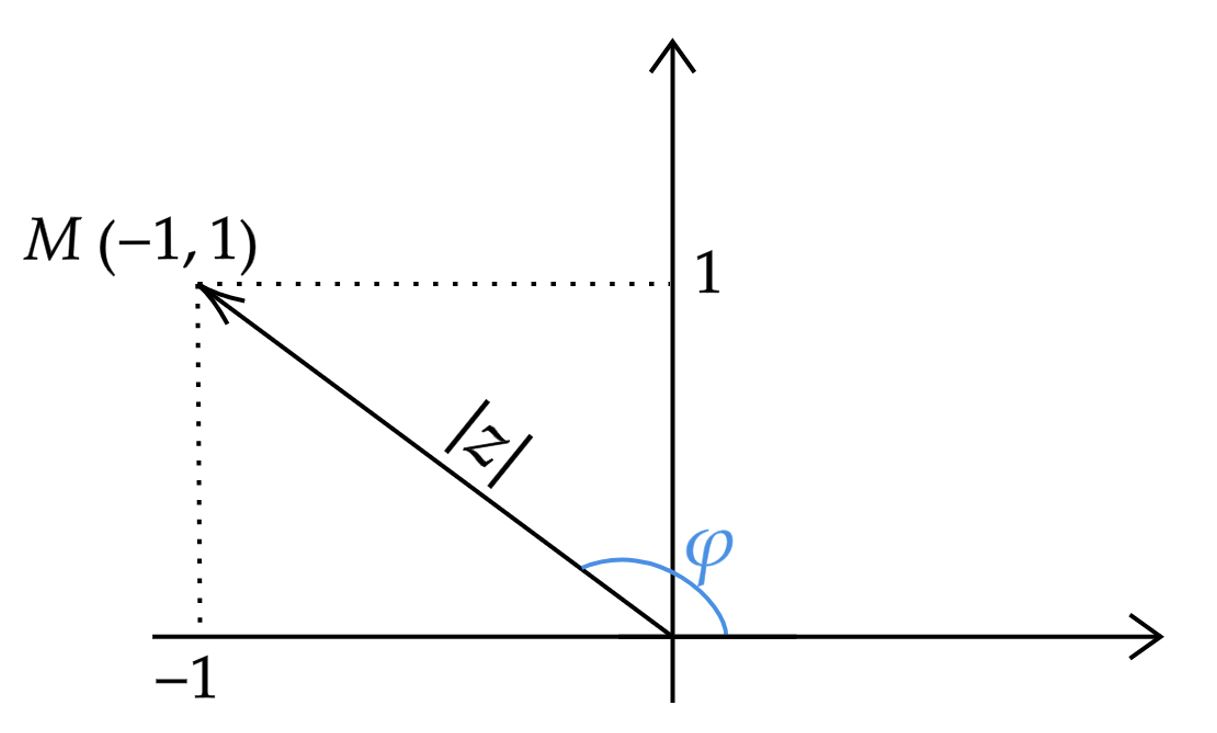Não é difícil encontrar: \begin{matrix} \fbox{$ \varphi = \frac{3\pi}{4} $} \end{matrix} $• \ \text{Alternativa (b):}$ Num raciocínio análogo ao anterior, na forma geométrica, temos: \begin{matrix} Z = (1,\sqrt{3}) &\Rightarrow& \varphi = 60^{\circ} \end{matrix} Já a forma trigonométrica pode ser escrita como, \begin{matrix} Z = r \ . \ (\cos{\varphi} + i\sin{\varphi}) \ \ , \ \ r = |Z| \\ \\ Z = r \ . \ (\frac{1}{2} + i\frac{\sqrt{3}}{2} ) \\ \\ r = 2 \end{matrix} Portanto, \begin{matrix} Z = 2 . (\cos{\frac{\pi}{3}} + i\sin{\frac{\pi}{3}}) \end{matrix}