Com a chave fechada e aberta, a diferença de potencial entre os pontos e é e a potência elétrica que as fontes fornecem ao circuito é .
Quando a chave está aberta e fechada, a corrente no resistor é .
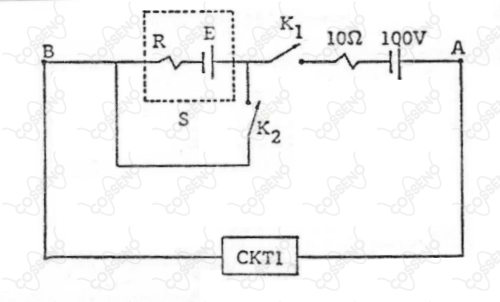
Determine o rendimento da fonte (não-ideal) quando a chave está fechada e aberta.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$-$ A priori, com $K_1$ fechada e $K_2$ aberta, têm-se a partir da potência elétrica fornecida ao circuito $CKT1$: \begin{matrix} Pot = \Delta V . i &\Rightarrow& 360 = 90.i_1 &\therefore& \fbox{$ i_1 = 4 \ A$}
\end{matrix}Pela $\text{Lei Generalizada de Ohm}$, temos: \begin{matrix} V_A - V_B = 100 - 10.i_1 + E - R.i_1 = 90 \ V &\Rightarrow& E = 30 + 4R & (1)
\end{matrix}
$-$ Já quando a chave $K_1$ é fechada, e $K_2$ aberta, constata-se: \begin{matrix} E = R.i_2 &\Rightarrow& E = 10R & (2)
\end{matrix}Substituindo $(2)$ em $(1)$: \begin{matrix} 10R = 30 + 4R &\therefore& \fbox{$ R =5 \Omega $} &,& \fbox{$ E = 50 \ V $}
\end{matrix}
$-$ Com esses resultados já podemos determinar o rendimento da fonte $S$, denotemos de $\Delta V$ a diferença de potencial da fonte $S$, então o rendimento $\eta$ : \begin{matrix} \eta = {\large{\frac{\Delta V }{E}}} = {\large{\frac{(E - R.i_1) }{E}}} = {\large{\frac{(50 - 20) }{50}}} &\therefore& \fbox{$ \eta = 60\% $}
\end{matrix}

