Um pequeno bloco $B$ de massa $0{,}002\ kg$ é mantido em repouso no alto de uma rampa pela tração de um fio isolante elétrico, ligado a uma carga elétrica positiva $Q$, de massa desprezível, afastada de $3 \times 10^{-3}\ m$ de uma carga negativa, de valor igual, ficada no fundo de um poço (ver a figura).
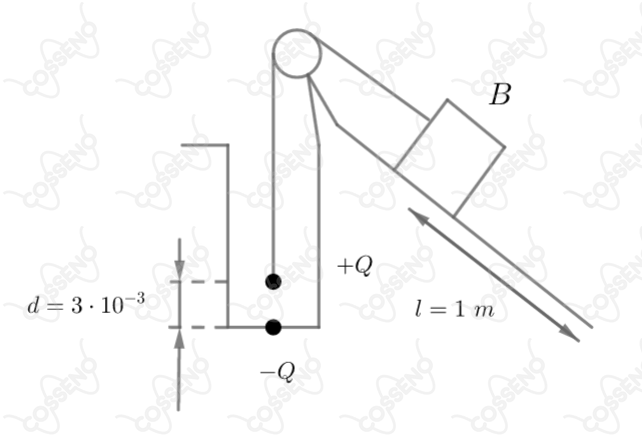
Calcule o valor das cargas sabendo que, se o fio for cortado, o bloco levará $2\ s$ para chegar ao fim da rampa, deslizando sem atrito (despreze a massa do fio).
Dado:
valor da constante da lei de Coulomb: $9 \times 10^9\ N\cdot m^2/C^2$
valor da constante da lei de Coulomb: $9 \times 10^9\ N\cdot m^2/C^2$
$-$ A priori, analisemos a situação que o fio é cortado, segundo a imagem do enunciado, a distância que bloco percorrerá até o fim da rampa será $1 \ m$. Além disso, não é difícil constatar também que sua aceleração será $a = g.\sin{\alpha}$ a partir da decomposição da força peso. Atente que, $\alpha$ é o ângulo de inclinação da rampa, enquanto $g$ é a aceleração da gravidade. Nesse viés, com conhecimento das equações horárias, sabemos que o bloco parte do repouso, então: \begin{matrix} 1 = 0.\Delta t + a. {\large{ \frac{\Delta t^2}{2}}} &\Rightarrow& g.\sin{\alpha} = {\large{ \frac{1}{2}}} &\therefore& \sin{\alpha} = {\large{ \frac{1}{20}}}
\end{matrix}$-$ Nessa perspectiva, já podemos analisar a situação inicial do enunciado, denotemos a tração de $T$, como o sistema está estático, a força de atração $(F_e)$ entre as cargas deve ser igual a tração, assim: \begin{matrix} T = F_e &\therefore& T = {\large{ \frac{K.Q^2}{d^2}}}
\end{matrix}Com isso, pensando agora no bloco, ao decompor a força peso temos outra relação de igualdade, esta que nos fornecerá o valor da carga $Q$, veja: \begin{matrix} T = P.\sin{\alpha} &\Rightarrow& {\large{ \frac{K.Q^2}{d^2}}} = 0,02.\sin{\alpha} &\therefore& |Q| = 10^{-9} \ C
\end{matrix}
