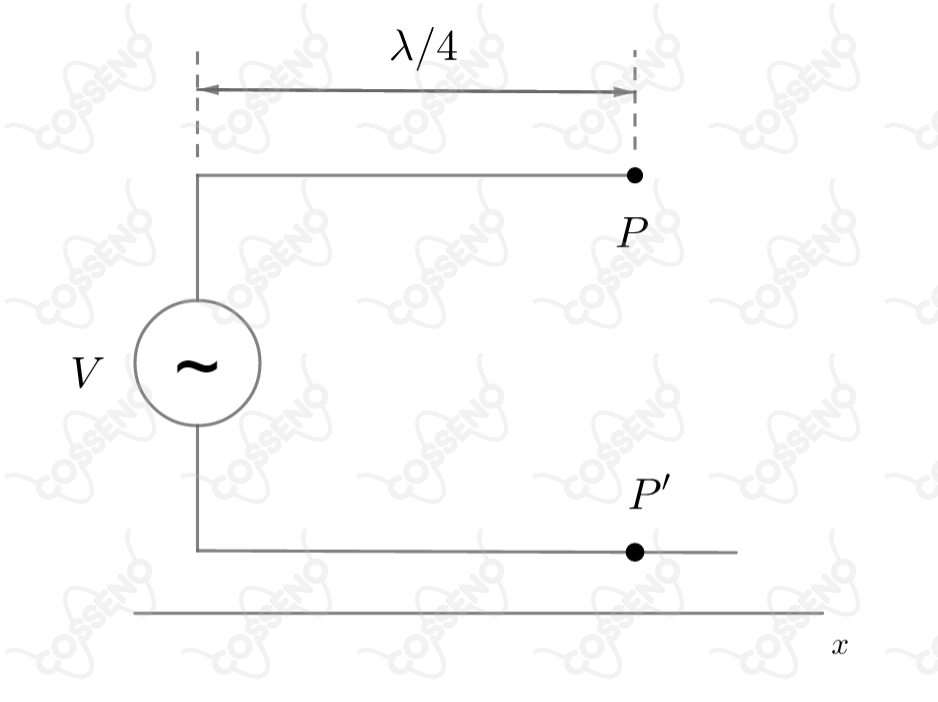
Uma diferença de potencial da forma é aplicada aos terminais de uma linha de transmissão sem perdas. Entre os pontos e , localizados a uma distância de um quarto da onda do início da linha (veja a figura), a diferença de potencial pode ser descrita por uma equação da forma . Determine os valores de e .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$-$ Analisando as expressões, façamos $t =0$ e $\lambda = 0$ : \begin{matrix} V(0,0) = V_m. \sin{0} &,& V(0,0) = A.\sin{0} + B.\cos{0} \\ \\ V(0,0) = 0 && V(0,0) = B
\end{matrix}Assim, \begin{matrix} B = 0 & \tiny{\blacksquare}
\end{matrix}
$-$ Agora, se $\lambda = 0$ : \begin{matrix} V(0,t) = V_m. \sin{wt} &,& V(0,t) = A.\sin{wt}
\end{matrix}Então, \begin{matrix} A = V_m & \tiny{\blacksquare}
\end{matrix}
$-$ Determinados os valores de $A$ e $B$, temos: \begin{matrix} \fbox{$ (A,B) = (V_m , 0) $}
\end{matrix}

