Um submarino inimigo encontra-se a uma altura do fundo do mar, numa região onde a gravidade vale e a água pode ser considerada um fluido não viscoso, incompressível, com massa específica . Subitamente, a nave solta do seu interior uma misteriosa caixa cúbica de volume e massa específica .
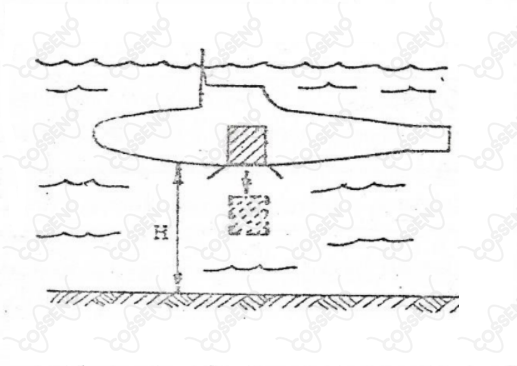
Determine o tempo que a caixa gasta até tocar o solo.
$g=10\ m/s^2$
$H=7{,}5\ m$
$\rho=1000\ kg/m^3$
$h=2\ m$
$H=7{,}5\ m$
$\rho=1000\ kg/m^3$
$h=2\ m$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$-$ Analisando as forças que atuam sobre a caixa, verifica-se que são duas, o peso $(P)$ e o empuxo $(E)$, logo, o módulo da aceleração que o bloco afunda é: \begin{matrix} F_r = P - E &\Rightarrow& m a = mg - \rho gh^3 &\Rightarrow& a = g (1 - {\large{\frac{\rho h^3}{m}}}) &,& m = 1,2 \rho h^3 &\therefore& a = {\large{\frac{5}{3}}} \ m/s^2
\end{matrix}Pela lei horária de um movimento retilíneo e uniformemente acelerado, têm-se:\begin{matrix} H = a {\large{(\frac{\Delta t^2}{2})}} &\Rightarrow& \Delta t = \sqrt{ {\large{\frac{2H}{a}}} } &\therefore& \Delta t = 3 \ s & \tiny{\blacksquare}
\end{matrix}

