A figura mostra um bloco "" de massa que parte do repouso em "" e desce o plano inclinado com atrito cujo coeficiente cinético é . Em "",o bloco "" choca-se com o bloco "" de massa , inicialmente em repouso. Com o choque, "” desloca-se na pista horizontal, desliza sobre sua parte semicircular e vai cair sobre o ponto "".
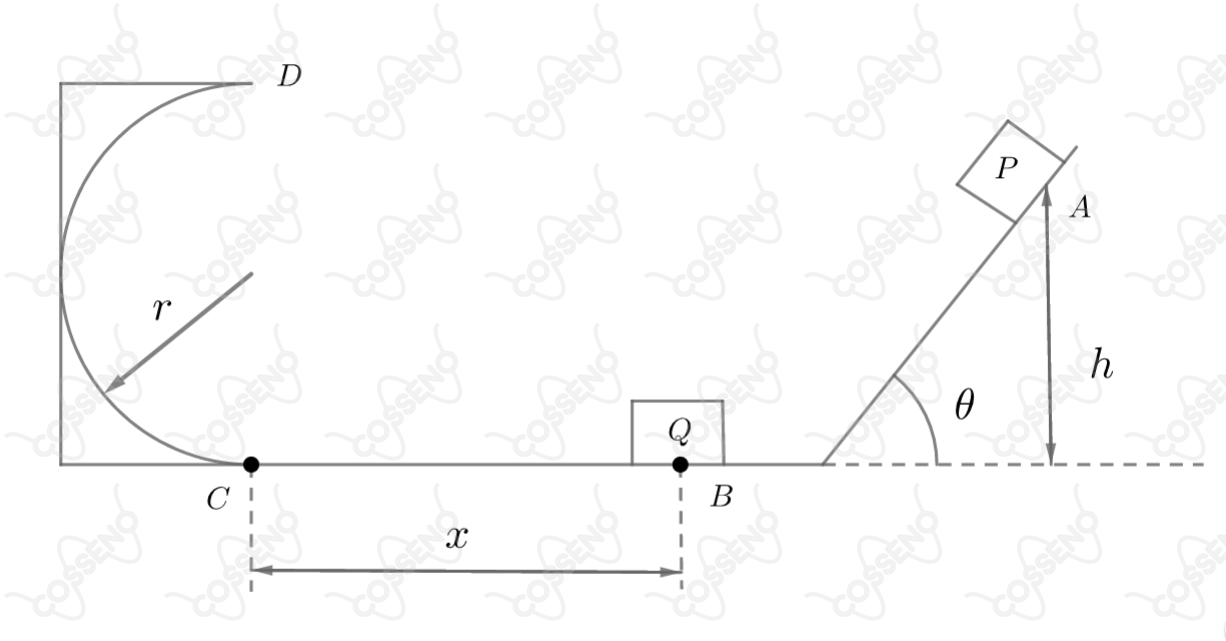
Sabendo que as partes horizontal e semicircular da pista não têm atrito e que o coeficiente de restituição entre "" e "" é , determine a altura "".
Dados:
$\quad g = 10\ m/s^2 \\\quad r = 2{,}5\ m\\\quad x = 2 \sqrt{11}\\\quad \theta = 45^{\circ}\\$
OBS: Despreze a resistência do ar e as dimensões dos blocos.
$\quad g = 10\ m/s^2 \\\quad r = 2{,}5\ m\\\quad x = 2 \sqrt{11}\\\quad \theta = 45^{\circ}\\$
OBS: Despreze a resistência do ar e as dimensões dos blocos.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$-$ Decompondo as forças que agem no bloco $P$ em seu momento inicial, pode-se encontrar a aceleração com que o bloco desce a rampa, esta que será útil para encontrar a velocidade com que o bloco $P$ colide com o bloco $Q$, faremos isso a partir da equação de Torricelli, veja: \begin{matrix} F_r = P\sin{\theta} - fat&\Rightarrow&M a = Mg\sin{\theta} - \mu Mg\cos{\theta} &\Rightarrow& a = g(\sin{\theta} - \mu \cos{\theta}) &\therefore& a = 4\sqrt{2} \ m/s^2
\end{matrix}Continuando, seja $v_0$ a velocidade que o bloco $P$ atinge o bloco $Q$: \begin{matrix} (v_0)^2 = 0^2 + 2a{\large{(\frac{h}{\sin{\theta}})}} &\therefore& \fbox{$(v_0)^2 = 4^2 h$}
\end{matrix}$-$ O enunciado informa que a colisão é parcialmente elástica, desse modo, deve-se elaborar a conservação da quantidade de movimento, e claro, o coeficiente de restituição: \begin{matrix} \begin{cases} \Delta \vec{P} = 0 &\Rightarrow& Mv_0 = Mv_1 + m u_0 &\Rightarrow& 5v_0 = 5v_1 + u\\
e = {\Large{\frac{u_0 - v_1}{v_0}}} &\Rightarrow& v_0 \cdot e = u_0 - v_1 &\Rightarrow& 4v_0 = 5u_0 - 5v_1 \end{cases} &\therefore& \fbox{$u_0 = {\large{\frac{3}{2}}}v_0$}
\end{matrix}Agora, com conhecimento da velocidade $u_0$ com que o bloco $Q$ parte até após a colisão, pode-se fazer a conservação da energia mecânica até o ponto $D$, em que o bloco sairá com velocidade $u_1$: \begin{matrix} \Delta E_M = 0 &\Rightarrow& {\large{\frac{m (u_0)^2}{2}}} = mg(2r) + {\large{\frac{m (u_1)^2}{2}}} &\therefore& (u_1)^2 = ({\large{\frac{3}{2}}}v_0)^2 - 4rg
\end{matrix}$-$ Por fim, o lançamento horizontal do bloco $Q$: \begin{matrix} x = u_1 \Delta t &,& \Delta t^2 = {\large{\frac{4r}{g}}} &\Rightarrow& x^2 = [({\large{\frac{3}{2}}}v_0)^2 - 4rg] {\large{\frac{4r}{g}}} &\Rightarrow& (v_0)^2 = 4^3 &\therefore& h = 4,0 \ m & \tiny{\blacksquare}\end{matrix}

