Uma barra condutora $MN$, de massa $m\ [kg]$ , de resistividade $\rho\ [\Omega\cdot m]$, submetida a uma tensão $V\ [V]$ entre suas extremidades, apoia-se em dois trilhos condutores e paralelos, que formam com a horizontal um ângulo $\alpha\ [^{\circ}]$.
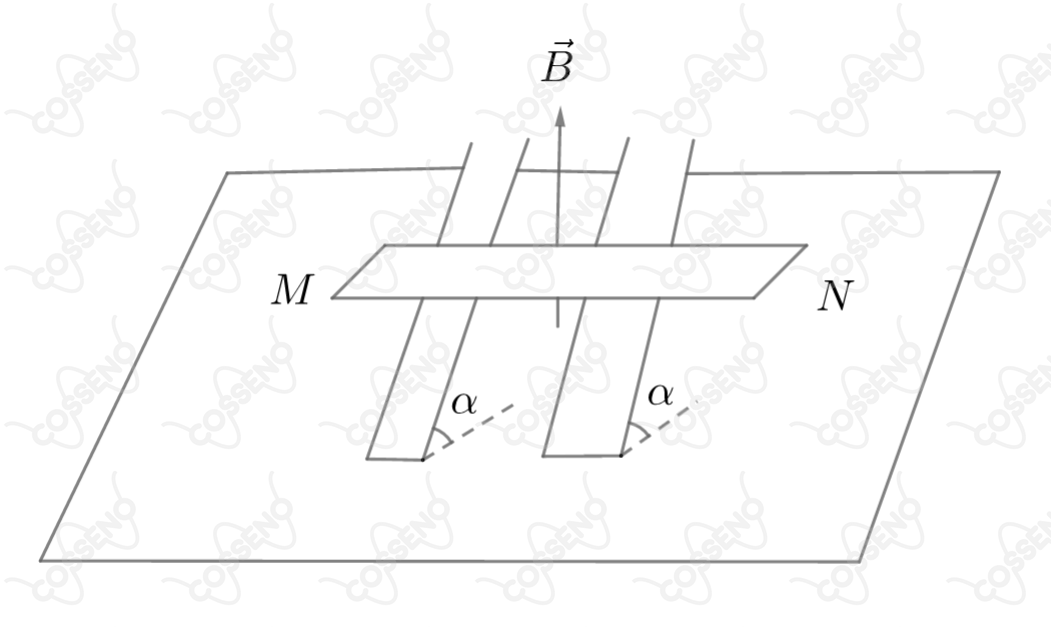
Não há atrito entre a barra e esses condutores e o conjunto está imerso em um campo magnético uniforme vertical, de intensidade $B\ [T]$.
A barra permanece em repouso na posição indicada. Determine:
a) o sentido da corrente na barra.
b) a seção reta da barra.
$• \ \text{a):}$ A priori, a barra tende a descer o trilho, assim, teremos uma força magnética atuando nos elétrons que compõem a barra. Atente que, pela regra da mão direita, os elétron "sentirão" uma força de sentido $M \rightarrow N$, consequentemente se deslocando nessa direção. Dessa forma, pode-se inferir que a corrente terá sentido $N \rightarrow M \ \tiny{\blacksquare}$
$• \ \text{b):}$ A partir das $\text{Leis de Ohm}$, temos: \begin{matrix} V = R.i &\Rightarrow& V = {\large{\frac{\rho . \overline{MN}}{S}}}.i &\therefore& S = {\large{\frac{\rho . \overline{MN}}{V}}}.i & (1)
\end{matrix}$\color{orangered}{Obs:}$ $S$ é a seção reta da barra.
Agora, tente imaginar ou esboçar a situação de um plano inclinado, conhecido o sentido da corrente, teremos a partir da regra da mão direita uma força magnética paralela ao plano horizontal, esta que será responsável por permanecer a barra em repouso. Nesse viés, ao decompor as forças podemos relacionar o peso a força magnética a partir da tangente, veja:
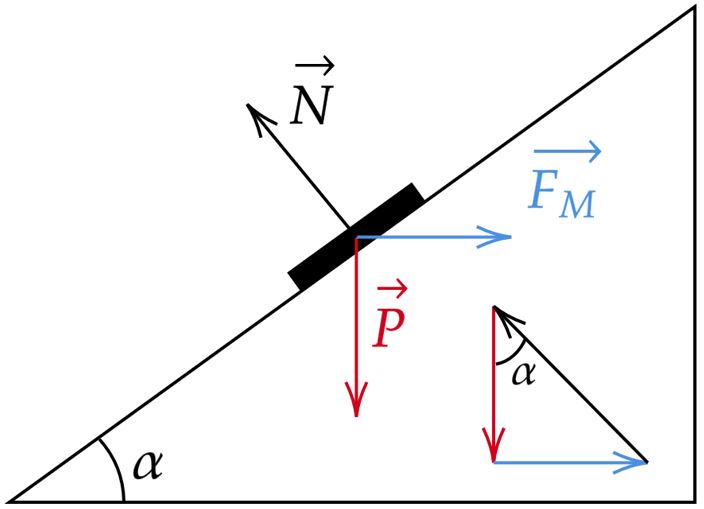\begin{matrix}
\tan{\alpha} = {\large{\frac{F_M}{P}}} = {\large{\frac{B.i.\overline{MN}}{m.g}}} &\therefore& i = {\large{\frac{m.g.\tan{\alpha}}{ B . \ \overline{MN}}}}
\end{matrix}Substituindo $i$ em $(1)$, têm-se: \begin{matrix} S = {\large{\frac{\rho . \overline{MN}}{V}}}.{\large{\frac{m.g.\tan{\alpha}}{ B . \ \overline{MN}}}} &\therefore& \fbox{$ S = {\large{\frac{\rho . m .g.\tan{\alpha}}{B.V}}} $}
\end{matrix}
Ampliar Imagem
Modo de Edição
0 / 5000