Um fio preso na extremidade O atravessa a argola fixa em A e sustenta um corpo de massa . A densidade linear de massa do fio é de . O corpo move-se formando um pêndulo cônico conforme a figura.
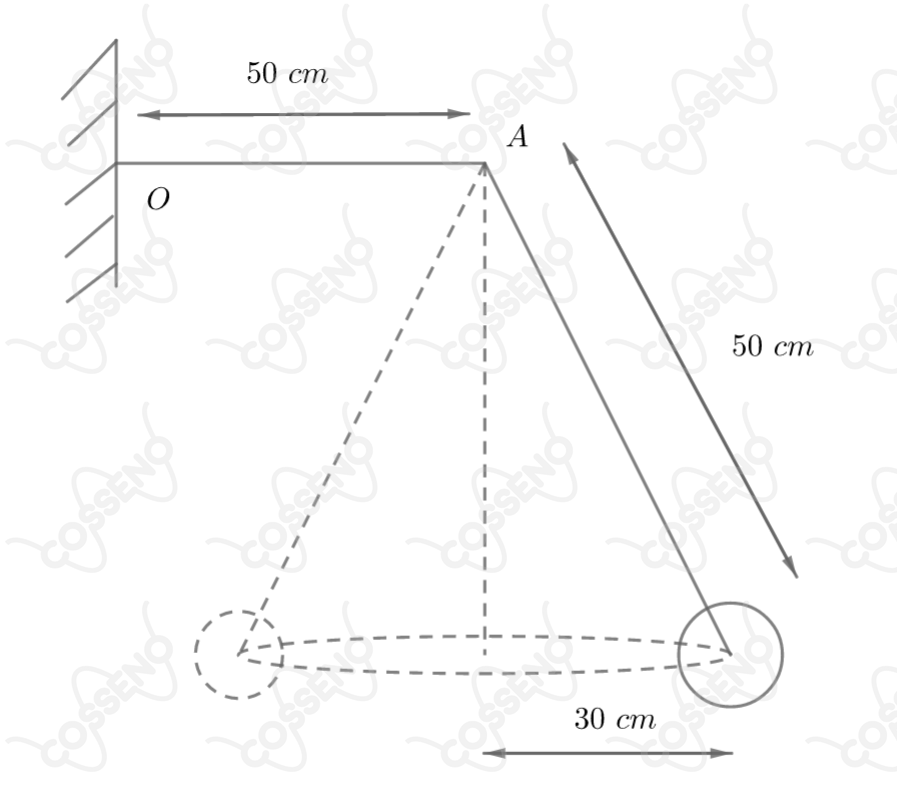
Determine a menor frequência possível para uma onda estacionária que oscile na parte horizontal do fio.
$g=10\ m/s^2$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

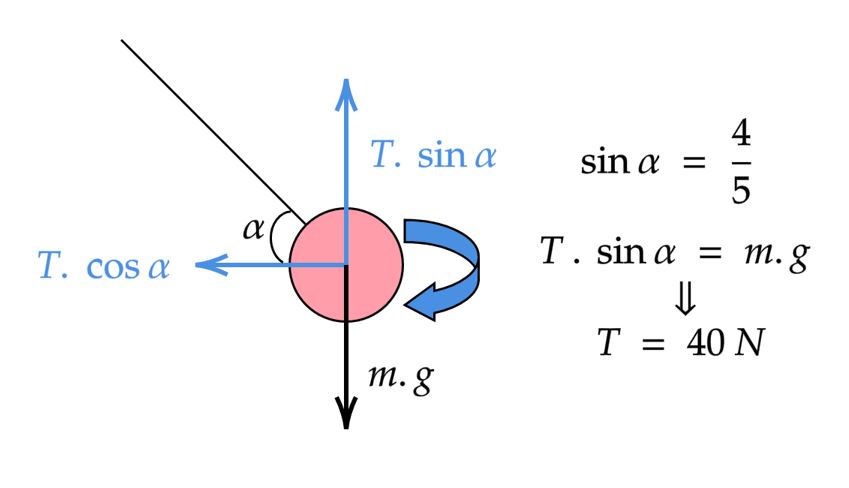
$-$ A priori, iremos encontrar o valor da tração ao fazer a análise de forças sobre o corpo, após isso, teremos como descobrir a velocidade de propagação da onda a partida da $\text{Equação de Taylor}$, então:
 \begin{matrix} v = \large{\sqrt{\frac{T}{\mu}}} &,& \mu = \large{\frac{m}{l}} &\Rightarrow& \fbox{$v = 100\ m/s$}
\end{matrix}
$\color{orangered}{Obs:}$ Não é difícil descobrir o seno do ângulo, veja que temos um triângulo retângulo na imagem do enunciado. Além disso, ele é pitagórico.
$-$ Agora, devemos determinar a frequência mínima de oscilação dessa onda estacionária, veja que no geral, podemos escrever:
\begin{matrix} L = N. \frac{\lambda}{2} &\Rightarrow& 0,50 = N. \frac{\lambda}{2} &\therefore& \fbox{$\lambda= \large{ \frac{1}{N}} $}
\end{matrix}
Pela equação fundamental da ondulatória, temos:
\begin{matrix} v = \lambda.f &\Rightarrow& 100 = f . \large{ \frac{1}{N}} &\therefore& f = 100.N
\end{matrix}
Note que $N \in \mathbb{N}^*$, logo, sua frequência mínima é a fundamental, isto é, $N=1$. Portanto:
\begin{matrix} \fbox{$f = 100\ Hz$}
\end{matrix}
\begin{matrix} v = \large{\sqrt{\frac{T}{\mu}}} &,& \mu = \large{\frac{m}{l}} &\Rightarrow& \fbox{$v = 100\ m/s$}
\end{matrix}
$\color{orangered}{Obs:}$ Não é difícil descobrir o seno do ângulo, veja que temos um triângulo retângulo na imagem do enunciado. Além disso, ele é pitagórico.
$-$ Agora, devemos determinar a frequência mínima de oscilação dessa onda estacionária, veja que no geral, podemos escrever:
\begin{matrix} L = N. \frac{\lambda}{2} &\Rightarrow& 0,50 = N. \frac{\lambda}{2} &\therefore& \fbox{$\lambda= \large{ \frac{1}{N}} $}
\end{matrix}
Pela equação fundamental da ondulatória, temos:
\begin{matrix} v = \lambda.f &\Rightarrow& 100 = f . \large{ \frac{1}{N}} &\therefore& f = 100.N
\end{matrix}
Note que $N \in \mathbb{N}^*$, logo, sua frequência mínima é a fundamental, isto é, $N=1$. Portanto:
\begin{matrix} \fbox{$f = 100\ Hz$}
\end{matrix}

Ampliar Imagem


