A intensidade da corrente elétrica em um condutor metálico varia, com o tempo, de acordo com o gráfico abaixo. Sendo a carga elementar de um elétron , determine:
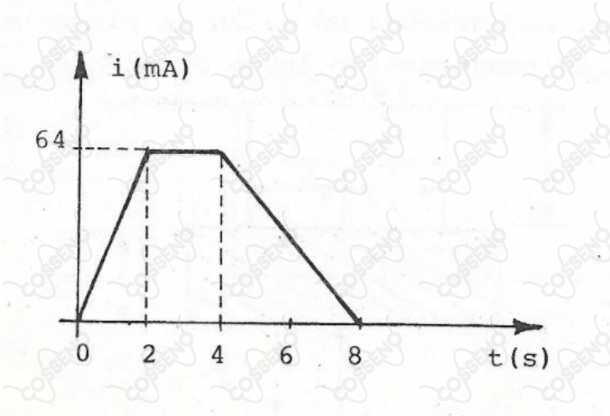
a) a carga elétrica que atravessa uma seção do condutor em segundos;
b) o número de elétrons que atravessa uma seção do condutor durante esse mesmo tempo;
c) a intensidade média de corrente entre os instantes zero e segundos.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$• \ \text{a):}$ A priori, sabemos que a carga elétrica é numericamente igual a área do polígono fechado, assim, identificamos facilmente um trapézio escaleno, logo: \begin{matrix} Q \overset{N}{=} {{\dfrac{(8+2)64}{2}}} = 320 \ \pu{mC} &\therefore& Q = 0,32 \ \pu{C}
\end{matrix}$• \ \text{b):}$ Com conhecimento que, $Q=n.e$ , em que $n$ é o número de elétrons, enquanto $e$ é a carga elementar, também podemos relacionar: \begin{matrix} n &=& {{\dfrac{\text{1 elétron}}{1,6\cdot 10^{-19} \ \pu{C}}}} \cdot 0,32 \ \pu{C} &\therefore& n =2\cdot 10^{18} \ \text{elétrons}
\end{matrix}$• \ \text{c):}$ Já sabemos a carga que atravessa a seção do condutor, nesse viés, a intensidade da corrente $i$: \begin{matrix} i = {{\dfrac{Q}{\Delta t}}} = {{\dfrac{0,32}{(8-0)}}} &\therefore& i =0,04 \ \pu{A}
\end{matrix}


