Uma placa infinitamente rígida encontra-se suspensa do teto por duas cordas elásticas de comprimento . Uma terceira corda, igualmente elástica e de comprimento , tem uma extremidade fixada à placa e outra submetida a uma força vertical . Num dado instante, um pulso horizontal é aplicado nesta última extremidade.
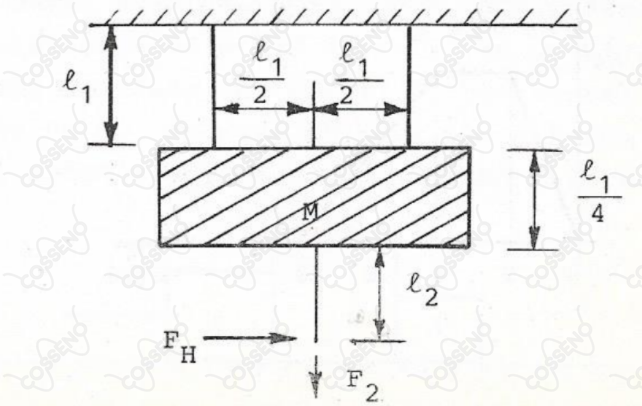
Determine o tempo transcorrido entre a aplicação do pulso e a chegada das ondas transversais no teto, considerando a massa das cordas desprezível na presença da massa da placa e uma tração constante ao longo das cordas.
Dados:
massa da placa: $M = 210 \ kg$
comprimento $l_1 = 0{,}5 \ m$
comprimento $l_2 = 1{,}0 \ m$
força $F_2 = 300 \ N$
aceleração da gravidade: $g = 10 \ m/{s}^{2}$
massa por unidade de comprimento das cordas: $\mu = 0{,}030 \ kg/m$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Nossa estratégia será calcular a velocidade de propagação dos pulsos em cada fio recorrendo à equação de Taylor: $$v=\sqrt{\dfrac{T}{\mu}}$$Sendo $T$ a tensão na corda e $\mu$ sua densidade linear.
Já conhecemos a tensão $F_2$ na corda de comprimento $l_2$, mas falta ainda calcular o módulo das forças de tensão $F_1$ nos fios de comprimento $l_1$. Como o sistema está em equilíbrio: $$\begin{align}2F_1&=P+F_2\\ F_1 &= \dfrac{2100 + 300}{2}\\ F_1&=\pu{1200 N}\end{align}$$
Assim, podemos calcular as velocidades $v_1$ e $v_2$ de propagação do pulso em cada corda: $$\begin{cases}v_1=\sqrt{\dfrac{F_1}{\mu}}=\sqrt{\dfrac{1200}{0{,}030}}=\pu{200 m/s}\\ v_2=\sqrt{\dfrac{F_2}{\mu}}=\sqrt{\dfrac{300}{0{,}030}}=\pu{100 m/s}\end{cases}$$
Assim, o tempo de propagação do pulso será a soma do tempo de propagação em cada corda: $$t = \dfrac{l_2}{v_2}+\dfrac{l_1}{v_1}\\ t = \dfrac{1}{100}+\dfrac{0{,}5}{200}=\boxed{\pu{0,0125 s}}$$
Podemos nos perguntar: mas o som não demora para atravessar a placa? Como o enunciado indica que "a placa é infinitamente rígida", o tempo de propagação de ondas mecânicas através da placa é desprezível!

