Um bloco desliza com velocidade constante sobre o trecho horizontal da pista e choca-se com o bloco , de mesma massa, inicialmente em repouso. Em consequência, o bloco desloca-se e, ao passar no ponto mais alto , não exerce qualquer esforço sobre a pista.
O bloco continua em movimento e chega a subir na parte curva da pista até uma altura de em relação ao trecho horizontal.
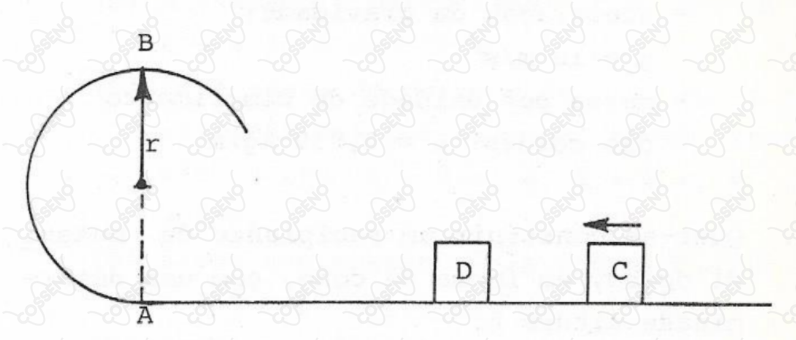
Desprezando a resistência do ar e o atrito entre as superfícies, determine a velocidade do bloco antes do choque.
Dados: $g = 10 \ m/{s}^{2}\quad ;\quad r = 2{,}88 \ m$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Sejam $V$ a velocidade do bloco $C$ antes do choque, $m$ as massas dos blocos e $U_C$, bem como $U_D$, respectivamente, as velocidades de $C$ e $D$ após o choque.
Primeiro, observemos a conservação de quantidade de movimento que ocorre antes e depois da colisão: $$m\cdot V = m\cdot U_C + m\cdot U_D \implies \color{yellow}{V = U_C + U_D}$$
Agora basta apenas calcular as velocidades $U$, a partir da conservação de energia no sistema. Assim, temos:
Bloco $C$: $\large{\frac{mU^2_C}{2} = mg\cdot 0,2}$ $\implies$ $\color{yellow}{U_C = 2}$ $\color{yellow}{m/s}$
Não só pela conservação de energia, e sim também por alguns conceitos de Dinâmica Rotacional. Quando se fala que $D$ não exerce nenhum esforço no ponto mais alto da curva, é o mesmo que dizer que a força normal ali é aproximadamente nula. Assim, temos:
Bloco $D$: $\large{\frac{mU^2_D}{2} = mg\cdot 2r + \frac{mU^2_{Df}}{2}}$ $\implies$ $\large{\frac{U^2_D}{2} = 2\cdot 28,8 + \frac{U^2_{Df}}{2}}$, e
$\large {mg = \frac{mU^2_{Df}}{2,88}}$ $\implies$ $U^{2}_{Df} = 28,8$ , temos: $U^2_{D} = 28,8\cdot 5$ $\implies$ $\color {yellow}{U_{D} = 12}$ $\color{yellow}{m/s}$
Portanto: $\large{\boxed {V = 2 + 12 = 14}}$, em $m/s$.

14:04 13/02/2026
Não, porque aí você vai misturar o que é energia com o que é qnt. de movimento. A relação não vale desse jeito. Mas, se trocar o mV por )mV2)/2 funciona.

14:25 15/04/2025
Não entendi muito bem. Mas eu poderia colocar que a quantidade de movimento inicial mV = mgHc + mgHd ? Porque depois da colisão a energia cinética de cada um virá potencial, não?

