A barra condutora com de comprimento, de peso e resistência elétrica desprezível, cai verticalmente com velocidade constante, fazendo contato com dois trilhos verticais, paralelos e sem atrito, com resistências também desprezíveis, conforme mostra a figura abaixo. Perpendicularmente ao plano dos trilhos existe um campo de indução magnética uniforme , com intensidade de .
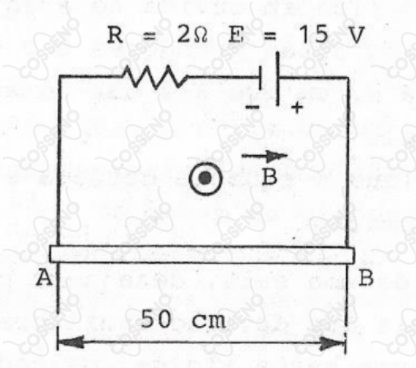
Determine:
a) a corrente na resistência
b) a velocidade da barra
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$• \ \text{a):}$ A priori, pela $\text{Lei de Lenz}$, sabemos que uma corrente elétrica induzida deve percorrer o sistema em prol de frear a variação do fluxo magnético. Atente que, a barra ao cair aumenta o fluxo do campo magnético saindo da tela, logo, pela regra da mão direita, teremos uma corrente de sentido horário, a fim de gerar um campo magnético contrário, isto é, entrando na tela. Nesse viés, já sabemos o sentido da corrente, e também do campo magnético segundo enunciado, assim, pela regra da mão direita (ou esquerda), nota-se uma força magnética contrária ao peso, estas forças que serão equivalentes, a fim de manter a velocidade da barra constante. \begin{matrix} F_M = P &\Rightarrow& B.i.L = 5 &\therefore& \fbox{$i = 20 \ A$}
\end{matrix}$\color{orangered}{Obs:}$ $L$ é o comprimento da barra.
$• \ \text{b):}$ Pelo raciocínio anterior, sabemos que essa variação de fluxo irá gerar uma $fme$ induzida, ou um gerador induzido, o denotemos de $\Large{\varepsilon}$, logo, do circuito: \begin{matrix} {\Large{\varepsilon}} =R.i - E &\therefore& {\Large{\varepsilon}} = 25 \ V
\end{matrix}Com isso, a partir da $\text{Lei de Faraday-Neumann}$: \begin{matrix} |{\Large{\varepsilon}}|= {\large{\frac{\Phi}{\Delta t}}} = {\large{\frac{B.A}{\Delta t}}} = {\large{\frac{B.L.x}{\Delta t}}} = B.L.v
\end{matrix}$\color{orangered}{Obs:}$ $x$ é a distância percorrida no intervalo de tempo $\Delta t$ \begin{matrix} v = {\large{ \frac{|{\Large{\varepsilon}} |}{B.L}}} &\therefore& \fbox{$ v = 100 \ m/s $}
\end{matrix}

