No circuito da figura abaixo, determinar os valores de e para os quais a corrente no galvanômetro é nula.
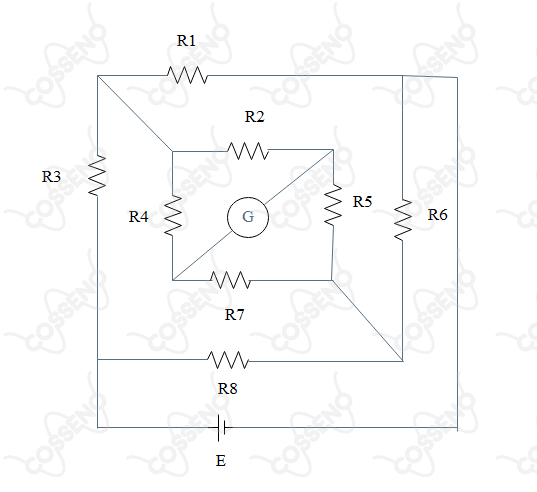
$R_1 = 10\ \Omega$
$R_2 = 3\ \Omega$
$R_3 = 20\ \Omega$
$R_4 = 6\ \Omega$
$R_5 = 2\ \Omega$
$R_6 = 15\ \Omega$
$E = 6\ V$
$R_2 = 3\ \Omega$
$R_3 = 20\ \Omega$
$R_4 = 6\ \Omega$
$R_5 = 2\ \Omega$
$R_6 = 15\ \Omega$
$E = 6\ V$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Questão muito interessante!
Na figura, conseguimos identificar que os resistores $R_2$, $R_4$, $R_5$ e $R_7$ formam uma ponte de Wheatstone.
Dessa forma, para que não passe corrente no galvanômetro $G$, temos 2 possibilidades:
1) A ponte obedece à condição de equilíbrio:$$R_2\cdot R_7 = R_4\cdot R_5\\ R_7 = \dfrac{6\cdot 2}{3}=\boxed{\pu{4 \Omega}}$$
2) Não exista diferença de potencial entre os extremos da ponte de Wheatstone. Para isso ocorrer, note que o circuito formado pelas resistências $R_1$, $R_3$, $R_6$ e $R_8$ também forma uma ponte de Wheatstone, então essa ponte externa deve também estar equilibrada. Assim:$$R_1\cdot R_8 = R_3\cdot R_6\\ R_8 = \dfrac{20\cdot 15}{10} = \boxed{\pu{30 \Omega}}$$
Bons estudos! 🚀

