A forma com que o circuito está desenhado pode enganar um pouco, mas o arranjo de resistências é bastante simples! Para ajudar a visualizar o circuito, vamos $\text{unir pontos de mesmo potencial}$. 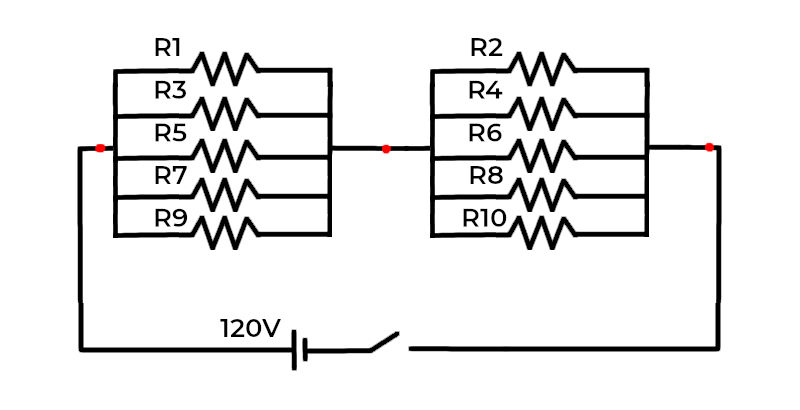A resistência equivalente será:$$R_{eq}=\left(R_1 \| R_3 \| R_5 \| R_7 \| R_9\right)+\left(R_2 \| R_4 \| R_6 \| R_8 \| R_{10}\right)\\ R_{eq}=\dfrac{1}{\frac{1}{320}+\frac{1}{80}+\frac{1}{80}+\frac{1}{160}+\frac{1}{320}}+\dfrac{1}{\frac{1}{320}+\frac{1}{640}+\frac{1}{80}+\frac{1}{160}+\frac{1}{640}}\\ R_{eq}=\dfrac{1}{\frac{3}{80}}+\dfrac{1}{\frac{2}{80}}\\ \boxed{R_{eq}=\frac{200}{3}\ \Omega}$$Então a corrente que sai da fonte é igual a $$I=\frac{V}{R_{eq}}=\frac{120}{\frac{200}{3}}=\boxed{1{,}8\ A}$$Agora, para determinar a corrente que passa em $R_3$, basta analisar o primeiro divisor de corrente da figura. Através do paralelo das resistências ímpares passa a corrente $I=1{,}8\ A$. A corrente será então dividida entre cada resistência de forma inversamente proporcional: mais corrente passa nos ramos de menor resistência. Mas podemos encontrar esse valor de uma forma ainda mais rápida: a corrente que passa por $R_3$ é igual à queda de tensão nessa resistência, dividida pelo valor da resistência. Ou seja:$$I_{R_3}=\frac{V_{R_3}}{R_3}=\frac{I \cdot R_{eq\, 1}}{R_3}=I\cdot \frac{R_{eq\, 1}}{R_3}\\ I_{R_3}=1{,}8\cdot \frac{\frac{80}{3}}{80}=\boxed{0{,}6\ A}$$Analogamente, para $R_8$:$$I_{R_8}=1{,}8\cdot \frac{\frac{80}{2}}{160}=\boxed{0{,}45\ A}$$