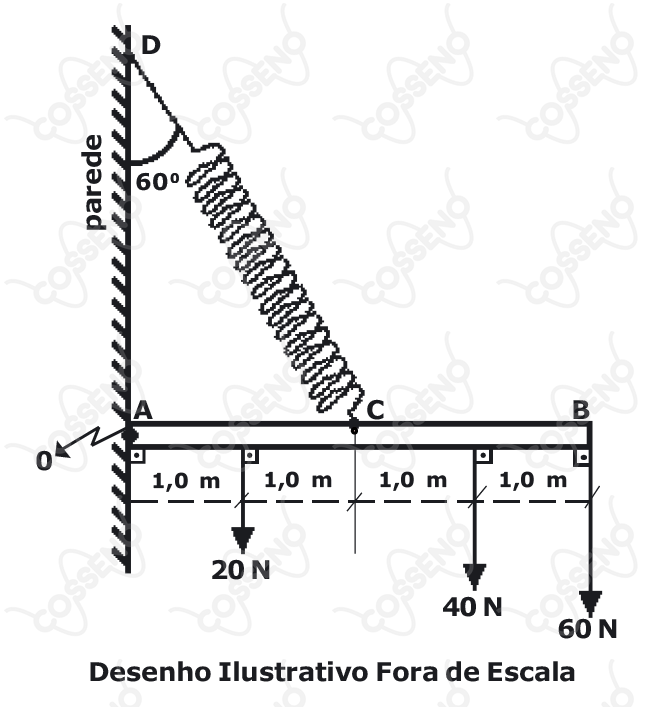
O ponto de uma haste homogênea , de seção reta uniforme com massa desprezível, está preso, através de uma mola ideal, ao ponto de uma parede vertical. A extremidade da haste está articulada em . A haste sustenta pesos de , e e está em equilíbrio estático, na horizontal, conforme representado no desenho abaixo. Sabendo que a deformação na mola é de , então o valor da constante elástica da mola é
$\begin{align} \sin 30º &= \cos 60º = \frac{1}{2} \\ \cos30º &= \sin60º = \frac{\sqrt{3}}{2} \end{align} $
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Seja $F_{el}$ a força elástica da mola e $k$ a constante elástica da mola.
Analisando o momento da força $F_{el}\cos60°$ , $20\text{N}$ , $40\text{N}$ e $60\text{N}$ podemos concluir que no equilíbrio estático temos
$F_{el}\cos60° \cdot 2= 20 \cdot 1 + 40 \cdot 3 + 60 \cdot 4 $
$= k \cdot 10 \cdot 10^{-2} \cdot \dfrac{1}{2} \cdot 2 = 20 + 120 + 240$
$= \dfrac{k}{10} = 380 \implies \boxed{k = 3800 \text{ N}/\text{m}} $
$\textbf{Resposta : Alternativa C}$

