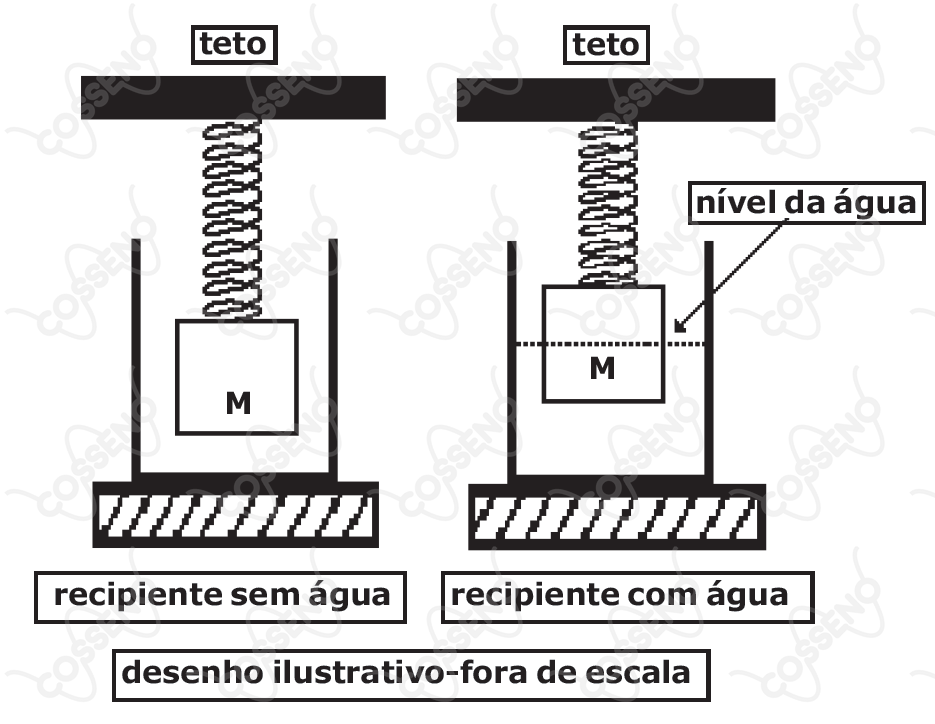
No interior de um recipiente vazio, é colocado um cubo de material homogêneo de aresta igual a e massa . O cubo está preso a uma mola ideal, de massa desprezível, fixada no teto de modo que ele fique suspenso no interior do recipiente, conforme representado no desenho abaixo. A mola está presa ao cubo no centro de uma de suas faces e o peso do cubo provoca uma deformação de na mola. Em seguida, coloca-se água no recipiente até que o cubo fique em equilíbrio com metade de seu volume submerso. Sabendo que a densidade da água é de , a deformação da mola nesta nova situação é de
Dado: intensidade da aceleração da gravidade $g=\pu{10 m/s2}$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$k$ a constante elástica da mola , $x$ a nova deformação da mola , $E$ o empuxo da água sobre o cubo , $\rho$ a densidade da água e $V$ o volume do cubo.
Analisando o caso em que o recipiente está sem água , podemos constatar que
$k \cdot (5\text{ cm}) = Mg = k \cdot (5 \cdot 10^{-2} \text{ m}) = 40 \text{ kg} \cdot 10 \text{ m}/ \text{s}$
$\implies k = 8000 \text{ N} / \text{m}$
Analisando o caso em que o recipiente está com água , poderemos encontrar que
$kx = Mg - E = (40 \cdot 10)\text{ N} - \rho \cdot \dfrac{V}{2} \cdot g = 8000 \cdot x$
$ = 400 - 1000 \cdot \dfrac{0,40^3}{2} \cdot 10 = 8000 \cdot x =400 - 320$
$\implies 8000x = 80 \implies x = \left(\dfrac{1}{100}\right)\text{ m}$
$ = \left(\dfrac{1}{100}\right) \cdot 100 \text{ cm} = \boxed{x = 1 \text{ cm}} $
$\textbf{Resposta : Alternativa E}$

