Uma fonte luminosa está fixada no fundo de uma piscina de profundidade igual a 1,33 m. Uma pessoa na borda da piscina observa um feixe luminoso monocromático, emitido pela fonte, que forma um pequeno ângulo com a normal da superfície da água, e que, depois de refratado, forma um pequeno ângulo com a normal da superfície da água, conforme o desenho. A profundidade aparente “h” da fonte luminosa vista pela pessoa é de:
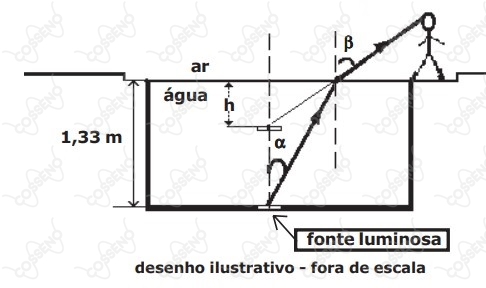
sendo os ângulos $\alpha$ e $\beta$ pequenos
considere $\tan{\alpha}\cong \sin{\alpha}$ e $tan{\beta} \cong \sin{\beta}$ indice de refração da água: $n_{água}= 1,33$ indice de refração do ar: $n_{ar}= 1$
considere $\tan{\alpha}\cong \sin{\alpha}$ e $tan{\beta} \cong \sin{\beta}$ indice de refração da água: $n_{água}= 1,33$ indice de refração do ar: $n_{ar}= 1$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Note que o ângulo de incidência do feixe luminoso monocromático é igual a $\alpha$ e o ângulo de refração é igual a $\beta$ , utilizando a Lei de Snell podemos escrever que
$n_{água} \cdot \sin \alpha = n_{ar} \cdot \sin \beta$
$= 1,33\sin \alpha = \sin \beta $
$\implies $
$1,33\tan \alpha \approx \tan \beta$
$\implies \dfrac{\tan \alpha}{\tan \beta} \approx \dfrac{1}{1,33}$
Seja $x$ a distância entre as duas normais representadas na figura , perceba que $\tan
\beta = \dfrac{x}{h}$ e $\tan \alpha = \dfrac{x}{1,33}$
$\therefore$
$x = h\tan \beta \implies \tan \alpha = \dfrac{h \tan \beta}{1,33} \implies h = \dfrac{1,33\tan \alpha}{\tan\beta} $
$\therefore$
$h \approx 1,33 \cdot \dfrac{1}{1,33}$
$\implies \boxed{h \approx 1 \text{ m}}$
$\textbf{Resposta : Alternativa B}$

