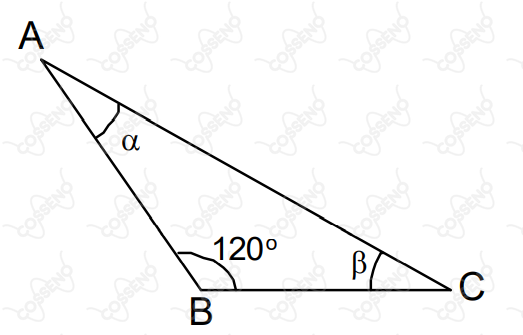
Da figura abaixo, sabe-se que . Então, o vale:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Como $\beta$ é um ângulo agudo e $\cos(\beta) = \dfrac{\sqrt{2}}{2}$ , logo $\beta = 45°$ , implicando dizer que $\alpha = 15°$.
$\cos(\alpha) =\cos(15°) = \cos(45°-30°) = \cos(45°)\cdot \cos(30°) + \sin(45°)\cdot \sin(30°) $
$= \dfrac{\sqrt{2}}{2} \cdot \dfrac{\sqrt{3}}{2} + \dfrac{\sqrt{2}}{2} \cdot \dfrac{1}{2}$
$ = \boxed{\cos(\alpha) = \dfrac{\sqrt{6}}{4} + \dfrac{\sqrt{2}}{4}}$
$\textbf{Resposta : Alternativa C}$
Sendo $\beta = 45°$, temos$$\alpha = 180°-120°-45° \implies \alpha = 15°$$Assim$$\cos \alpha = \cos 15° = \cos \dfrac{30°}{2} = \sqrt{\dfrac{1+\frac{\sqrt{3}}{2}}{2}} \implies \cos \alpha = \dfrac{\sqrt{2+\sqrt{3}~}}{2}$$Portanto$$\cos \alpha = \dfrac{2}{2}\cdot \dfrac{\sqrt{2+\sqrt{3}~}}{2} = \dfrac{\sqrt{8+2\sqrt{12}~}}{4}~=~\dfrac{\sqrt{\left(\sqrt{6}+\sqrt{2}\right)^2~}}{4}$$$$\boxed{\cos \alpha = \dfrac{\sqrt{6}+\sqrt{2}}{4} = \dfrac{\sqrt{6}}{4}+\dfrac{\sqrt{2}}{4}}$$$$\bf{Alternativa ~(C)}$$

20:03 18/01/2024
por que o cos15° é raiz de 1+ raiz de 3/2 divido por 2 ? n seria só raiz de 3/2 divido por 2 ?


