Em um local onde a aceleração da gravidade é , as partículas idênticas, e , são lançadas simultaneamente, e sobem sem atrito ao longo dos planos inclinados e , respectivamente, conforme figura a seguir.
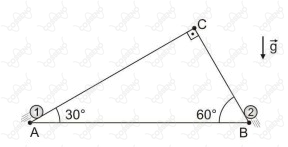
A partícula é lançada do ponto com velocidade e gasta um tempo para chegar ao ponto
Considerando que as partículas e colidem no vértice , então a velocidade de lançamento da partícula vale
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Para as partículas $1$ e $2$ colidirem em $C$ temos que o tempo de chegada ao ponto $C$ de ambos deve ser o mesmo , ou seja , a partícula $A$ e $B$ gastam um tempo $t$ para chegar ao ponto $C$. Seja $h$ a altura do triângulo , $v$ a velocidade inicial da partícula $1$ , $v_{c_{1}}$ a velocidade da partícula $1$ no ponto $C$ e $v_{c_{2}}$ a velocidade da partícula $2$ no ponto $C$ , perceba que a energia mecânica durante a subida se conserva para ambos por não haver forças dissipativas , logo a energia mecânica inicial é igual a energia mecânica no ponto $C$ para ambas partículas , portanto :
Aplicando a conservação da energia mecânica para a partícula $1$ :
$E_{i_{{1}}} = E_{c_{1}}$
$\dfrac{m(v)^2}{2} = \dfrac{m(v_{c_{1}})^2}{2} + mgh \implies (v)^2 = (v_{c_{1}})^2+ 2gh$
$\implies 2gh = (v)^2 - (v_{c_{1}})^2$
Aplicando a conservação da energia mecânica para a partícula $2$ :
$E_{i_{{2}}} = E_{c_{2}}$
$\dfrac{m(v_{0})^2}{2} = \dfrac{m(v_{c_{2}})^2}{2} + mgh \implies (v_{0})^2 = (v_{c_{2}})^2+ 2gh$
$\implies 2gh = (v_{0})^2 - (v_{c_{2}})^2$
Concluindo-se que :
$(v)^2 - (v_{c_{1}})^2 = (v_{_{0}})^2 - (v_{c_{2}})^2 $
Note que a aceleração atuante sobre a partícula $A$ durante a subida é igual a $-\dfrac{g}{2}$ e a aceleração atuante sobre a partícula $B$ durante a subida é igual a $-\dfrac{\sqrt{3}}{2}g$ , logo , temos que
$v_{c_{1}} = v -\dfrac{g}{2}t $ $\land$ $v_{c_{2}} = v_{0} -\dfrac{g\sqrt{3}}{2}t $
$\therefore$
$(v)^2 - (v_{c_{1}})^2 = (v_{_{0}})^2 - (v_{c_{2}})^2 $
$(v)^2 - \left(v -\dfrac{g}{2}t \right)^2 = (v_{_{0}})^2 - \left(v_{0} -\dfrac{g\sqrt{3}}{2}t \right)^2 $
$ (v)^2 - \left((v)^2 - v(gt) + \dfrac{(gt)^2}{4}\right) =(v_{_{0}})^2 - \left((v_{0})^2 - \sqrt{3}v_{0}(gt) + \dfrac{3(gt)^2}{4}\right) $
$ \cancel{(v)^2} - \cancel{(v)^2} + v(gt) -\dfrac{(gt)^2}{4} =\cancel{(v_{_{0}})^2} -\cancel{(v_{0})^2} + \sqrt{3}v_{0}(gt) - \dfrac{3(gt)^2}{4} $
$v\cancel{(gt)} -\dfrac{(gt)^{\cancel{2}}}{4} = \sqrt{3}v_{0}\cancel{(gt)} - \dfrac{3(gt)^{\cancel{2}}}{4} $
$v -\dfrac{gt}{4} = \sqrt{3}v_{0} - \dfrac{3gt}{4}$
$\implies v = \sqrt{3}v_{0} - \dfrac{gt}{2} $
Considerando $g = 10m/s^2$ temos que
$v = \sqrt{3}v_{0} - \dfrac{gt}{2} = v = \sqrt{3}v_{0} - \dfrac{10t}{2}$
$= \boxed{v = \sqrt{3}\cdot v_{0} - 5t}$
$\textbf{Resposta : Letra A}$

