Três partículas, , e , movimentam-se, com velocidades constantes, ao longo de uma mesma direção. No instante inicial, , a distância entre e vale , e entre e vale , conforme indica a figura a seguir.
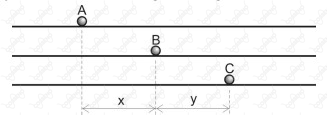
Em , a partícula cruza com a partícula . Em , a partícula cruza com a partícula . A partícula alcançará a partícula B no instante dado pela relação
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Adote o sentido de movimento de $A$ para a direita e o sentido de movimento de $B$ e $C$ para a esquerda.
Podemos calcular o valor de $x$ pela relação $x = V_{AB} \cdot t_{AB}$ , em que $V_{AB}$ é a velocidade relativa de $A$ em relação a $B$ e $t_{AB}$ é o tempo em que a partícula $A$ cruza com a partícula $B$.
$\therefore$
$x = V_{AB} \cdot t_{AB} = (V_{A} - (-V_{B})) \cdot 2 = x = 2(V_{A} + V_{B})$
De forma análoga o valor de $x + y$ pode ser calculada pela relação $x = V_{AC} \cdot t_{AC}$ , em que $V_{AC}$ é a velocidade relativa de $A$ em relação a $C$ e $t_{AC}$ é o tempo em que a partícula $A$ cruza com a partícula $C$.
$\therefore$
$x + y = V_{AC} \cdot t_{AC} = (V_{A} - (-V_{C})) \cdot 3 = x + y = 3(V_{A} + V_{C})$
Dessa duas equações podemos concluir que :
$2(x + y) - 3x = 6V_{A} + 6V_{C} - 6V_{A} - 6V_{B} = 2y - x = 6(V_{C} - V_{B})$
$\implies V_{C} - V_{B} = \dfrac{2y - x}{6}$
O problema consiste em calcular o valor de $t_{CB}$(tempo em que a partícula $C$ alcançará a partícula $B$) , note que podemos escrever que $t_{CB} = \dfrac{y}{V_{CB}}$ , em que $V_{CB}$ é a velocidade relativa de $C$ em relação a $B$.
$\therefore$
$t_{CB} = \dfrac{y}{V_{CB}} = \dfrac{y}{(V_{C} - V_{B})} = y \cdot \dfrac{6}{2y- x}$
$\implies \boxed{t_{CB} = \dfrac{6y}{2y - x}}$
$\textbf{Resposta : Alternativa A}$

