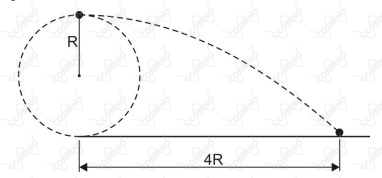
Uma partícula de massa , presa na extremidade de uma corda ideal, descreve um movimento circular acelerado, de raio , contido em um plano vertical, conforme figura a seguir.Quando essa partícula atinge determinado valor de velocidade, a corda também atinge um valor máximo de tensão e se rompe. Nesse momento, a partícula é lançada horizontalmente, de uma altura , indo atingir uma distância horizontal igual a . Considerando a aceleração da gravidade no local igual a , a tensão máxima experimentada pela corda foi de
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Da $2°$ Lei de Newton, sendo $v$ a velocidade da partícula no ponto de tensão $T$ máxima, temos:$$T + mg = \dfrac{mv^2}{R}$$
Após o rompimento, a partícula descreve um lançamento horizontal, e leva, a uma altura $2R$, um tempo $t$ para chegar ao solo, tal que:$$2R = \dfrac{gt^2}{2} \implies t = 2\sqrt{\dfrac{R}{g}~}$$Já conhecendo a distância percorrida pela partícula, temos:$$4R = v\cdot t \implies v^2 = 4gR$$
Assim:$$T + mg = \dfrac{4mgR}{R} \implies \boxed{T = 3mg}$$
$$\pu{Alternativa } \mathbb{(C)}$$
A tração máxima $T$ é dado por $T = \dfrac{mv_{x}^2}{R} - mg$ , onde $v_{x}$ é a velocidade da partícula bem antes do rompimento.
Analisando o movimento oblíquo da partícula na horizontal temos que $4R = v_{x}t \implies v_{x} = \dfrac{4R}{t} \implies v_{x}^2 = \dfrac{16R^2}{t^2}$ , onde $t$ é o tempo de descida da partícula.
Analisando a vertical temos que
$2R = \dfrac{gt^2}{2} \implies t^2 = \dfrac{4R}{g}$
$\therefore$
$v_{x}^2 = \dfrac{16R^2}{t^2} = v_{x}^2 =16R^2 \cdot \dfrac{g}{4R} = v_{x}^2 = 4Rg$
$\therefore$
$T = \dfrac{mv_{x}^2}{R} - mg = T = \dfrac{m \cdot 4Rg}{R} - mg = \boxed{T = 3mg}$
$\textbf{Resposta : Alternativa C}$



