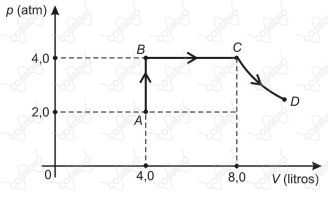
Uma amostra de mols de gás ideal sofre as transformações (isovolumétrica), (isobárica) e (isotérmica) conforme representação no diagrama pressão (p) volume (V), mostrado a seguir.
Sabendo-se que a temperatura do gás no estado é , pode-se afirmar que a temperatura dele, em , no estado é
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Considerações:
- $1~\pu{atm\cdot L} \approx 100~\pu{J}$ ;
- A temperatura em $D$ é a mesma que em $C$. Foquemos portanto em calcular a variação da temperatura desde $A$ até $C$ .
- Quando usadas, $T_A = 300~\pu{K}$, $T_B$ $\text{e}$ $T_C = T_D$, representarão, respectivamente, as temperaturas nos pontos $A$, $B$, $C$ e $D$ .
Equação de estado em $A$ : $800~J = nR\cdot 300~\implies~\color{green}{nR = 8/3}$
Equação de estado em $B$ : $1600~J = nR\cdot T_B~\implies ~ \color{green}{T_B = 600~\pu{K}}$
Agora, no processo $BC$, temos que o trabalho realizado pelo gás é$$1600~J = nR\cdot (T_C - T_B) \implies T_C = 1200~\pu{K} \implies \boxed{T_C = 927~° C}$$
$$\text{Alternativa } \mathbb{(D)}$$
Usando a equação de Clapeyron temos que
$\dfrac{P_{A} \cdot V_{A}}{T_{A}} = \dfrac{P_{C} \cdot V_{C}}{T_{C}}$
Note que pelo fato de a transformação $CD$ ser isotérmica temos que $T_{C} = T_{D}$
$\therefore$
$\dfrac{P_{A} \cdot V_{A}}{T_{A}} = \dfrac{P_{C} \cdot V_{C}}{T_{D}}$
$\dfrac{2 \cdot 4}{(27 + 273)\text{ K}} = \dfrac{4 \cdot 8}{T_{D}}$
$\implies T_{D} = 1200 \text{ K} = \boxed{T_{D} = 927 \text{ °C}}$
$\textbf{Resposta : Alternativa D}$


