Dispõe-se de quatro polias ideais de raios e que podem ser combinadas e acopladas a um motor cuja frequência de funcionamento tem valor .
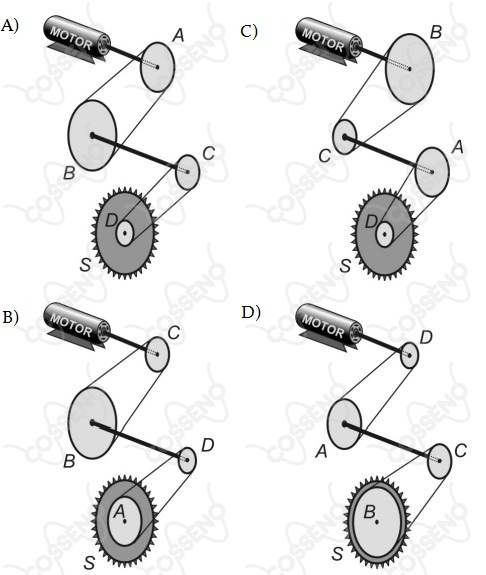
As polias podem ser ligadas por correias ideais ou unidas por eixos rígidos e, nos acoplamentos, não ocorre escorregamento. Considere que a combinação dessas polias com o motor deve acionar uma serra circular () para que ela tenha uma frequência de rotação igual a da frequência do motor. Sendo assim, marque a alternativa que representa essa combinação de polias
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Polias unidas por uma mesma correia têm a mesma velocidade tangencial em suas extremidades: $$v_1=v_2\\ \omega_1R_1 = \omega_2R_2\\ f_1R1 = f_2R_2$$
Já polias que têm um eixo de rotação comum têm a mesma velocidade angular (ambas levam o mesmo tempo para realizar uma revolução): $$\omega_1=\omega_2\\ f_1=f_2$$
Assim, vamos analisar cada arranjo para garantir que $f_S = 5f/3$, sendo $f_S$ a frequência da serra e $f$ a frequência do motor.
Alternativa a)
$f_A=f$ por estar conectada ao eixo do motor.
$f_B=\dfrac{R_A}{R_B}f_A$ pois estão conectados por uma correia.
$f_C = f_B$ pois têm mesmo eixo de rotação.
$f_D=\dfrac{R_C}{R_D}f_C$ pois estão conectados por uma correia.
$f_S = f_D$ pois têm mesmo eixo de rotação.
Assim, $f_S = \dfrac{R_A}{R_B}\cdot \dfrac{R_C}{R_D}\cdot f=\dfrac{5}{3}f$
Alternativa b)
$f_C=f$ por estar conectada ao eixo do motor.
$f_B=\dfrac{R_C}{R_B}f_C$ pois estão conectados por uma correia.
$f_D = f_B$ pois têm mesmo eixo de rotação.
$f_A=\dfrac{R_D}{R_A}f_D$ pois estão conectados por uma correia.
$f_S = f_A$ pois têm mesmo eixo de rotação.
Assim, $f_S = \dfrac{R_D}{R_A}\cdot \dfrac{R_C}{R_B}\cdot f=\dfrac{1}{60}f$
Encontramos a resposta! $\boxed{\text{Gabarito a)}}$
A análise das alternativas c) e d) também poderia ser feita de forma análoga às anteriores. Encontraríamos $f_S=60f$ e $f_S=f/60$, respectivamente.

