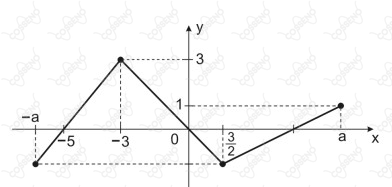
Na figura abaixo, está representado o gráfico da função real , onde
Analise as alternativas abaixo e marque a INCORRETA.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$A)$ sendo $\text{Im} ~(f)~=~\left[-\frac{3}{2}~,~3\right]$ bem como $h(x) = f(x)+\frac{3}{2}$, então $$\text{Im} ~(h)~=~\text{Im} ~(f)+\dfrac{3}{2}~=~\left[-\frac{3}{2}+\frac{3}{2}~,~3+\frac{3}{2}\right] \implies \text{Im} ~(h)~=~\left[0~,~\frac{9}{2}\right]$$
$B)$ ao observar o gráfico $f$ percebe-se que $f(x) = -x$ para todo $x \in \left[-3,\frac{3}{2}\right]$, assim$$s(0)~=~f\left(\frac{3}{2}\right)~=~-\dfrac{3}{2}$$
$C)$ quando $x \in \left[-a,-3\right]$ tem-se $f(x) = \dfrac{3x}{2}+\dfrac{15}{2}$ tal que$$f(-a) = -\dfrac{3a}{2}+\dfrac{15}{2}=-\dfrac{3}{2} \implies \color{red}{a = 6}\\\color{system}{\text{Dom}~(r)}~=~\text{Dom}~(f) \implies \text{Dom}~(r)~=~[-6,6]$$
$D)$ sendo $\text{Im} ~(f)~=~\left[-\frac{3}{2}~,~3\right]$ bem como $r(x) = f(x)-3$, então $$\text{Im} ~(r)~=~\text{Im} ~(f)-3~=~\left[-\frac{3}{2}-3~,~3-3\right] \implies \text{Im} ~(r)~=~\left[-\frac{9}{2}~,~0\right]$$percebamos que o $\{0\} \in \text{Im}~(f)$ e o $x$ correspondente ao limite superior permanece o mesmo da função original, isto é, $r(-3) = 0$.
$\bf{Conclusão}$: a $D)$ é falsa, pois afirma que não há raízes reais, quando na verdade tem.$$\bf{Alternativa~(D)}$$

