Uma esfera metálica de peso está presa a uma das extremidades de um fio de massa desprezível, cuja extremidade oposta está ligada a um suporte fixo. Sabendo-se que o sistema está em equilíbrio, em uma posição na qual o fio forma com a vertical um ângulo ?, equilíbrio este conseguido pela ação de uma força horizontal aplicada à esfera, pode-se afirmar que o módulo de tal força é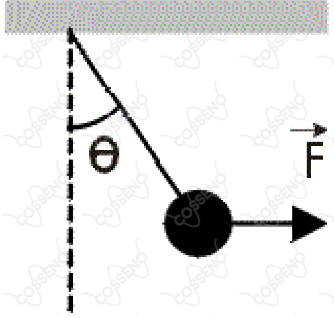
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Determinando os eixos-padrão, decompõe-se a tração T do fio em duas componentes, de modo que:
$(i)$ $P=T\cdot \cos {\theta}$ e $(ii)$ $F=T\cdot \sin {\theta}$
Em $(i)$, temos: $T=\frac{P}{\cos {\theta}}$, logo, substituindo na equação $(ii)$, temos:
$F=\frac{P}{\cos {\theta}} \cdot \sin {\theta}$ $\implies$ $\boxed {F= P \cdot \tan {\theta}}$
Alternativa $(\mathbb {A})$
Ampliar Imagem
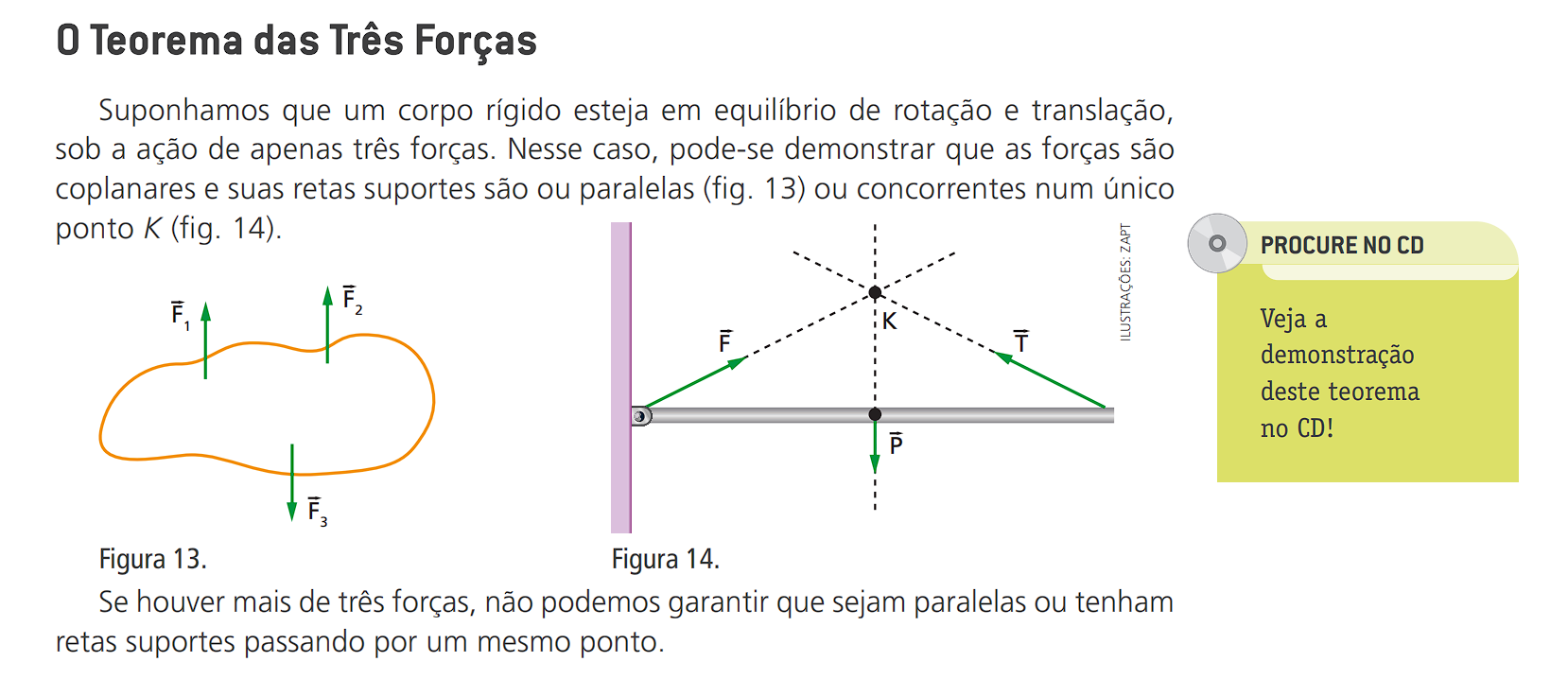
As forças atuantes sobre a esfera é a tração $T$ do fio , o seu peso $P$ e a força $F$.
Realizando a decomposição da força $T$ podemos constatar que na horizontal teremos que
$F = T\sin\theta$
Na vertical temos
$T\cos\theta = P \implies T = \dfrac{P}{\cos\theta}$
$\therefore$
$F = T\sin\theta = \dfrac{P}{\cos\theta} \cdot \sin\theta = \boxed{F = P\tan\theta}$
$\textbf{Resposta : Alternativa A}$



