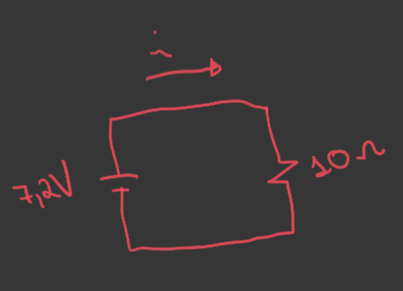
$U=\varepsilon-r_{int}.i$ como rendimento é de 60%: $U=\varepsilon.\frac{60}{100}$ $U=12.\frac{60}{100}$ $U=7,2V$ Montando um pequeno circuito para simular o exposto no enunciado: $U=r.i$ $7,2=10.i$ $i=0,72$ $U =\varepsilon-r_{int}.i $ $7,2=12-r_{int}.0,72$ $r_{int}=\frac{4,8}{0,72}=6,666$ Alternativa C

Adote um circuito simples que contêm apenas $1$ gerador e $1$ receptor. Seja $\epsilon$ a força eletromotriz do gerador ,$P_{total}$ a potência total oferecida pelo gerador , $Pot_{u}$ a potência útil do gerador , $i$ a corrente que percorre o circuito , $R$ a resistência do receptor e $r$ a resistência interna desejada. A priori devemos saber que $U_{u} = \epsilon - ri$ e que $U_{u} = Ri$. $\therefore$ $ \epsilon - ri = Ri \implies \epsilon = (r + R)i$ O rendimento $K$ do gerador é definido como $K = \dfrac{Pot_{u}}{Pot_{total}}$. $\therefore$ $K = \dfrac{Pot_{u}}{Pot_{total}} = K = \dfrac{U_{u}}{\epsilon} \implies U_{u} = K\epsilon = Ri$ $\implies i = \dfrac{K\epsilon}{R}$ $\therefore$ $\epsilon = (r + R) \cdot \dfrac{K \epsilon}{R} \implies R = (r + R)K$ $\implies r = \dfrac{R(1 - K)}{K}$ Substituindo os valores temos que $ r = \dfrac{10(1 - 60\%)}{60\%} = \dfrac{40\% R}{60 \%} = \dfrac{40 \cdot 10}{60} = r = \dfrac{20}{3} = \boxed{r \approx 6,7 \Omega} $ $\textbf{Resposta : C}$