Um bloco de é empurrado sobre um assoalho horizontal por uma força que faz um ângulo de com a horizontal, conforme mostra a figura abaixo. O coeficiente de atrito entre o bloco e o assoalho é . O valor da força , em newtons, necessária para colocar o bloco na iminência de deslizar é, aproximadamente,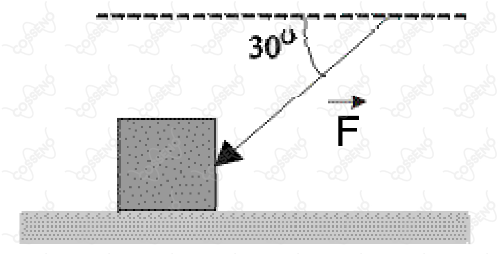
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Ampliar Imagem
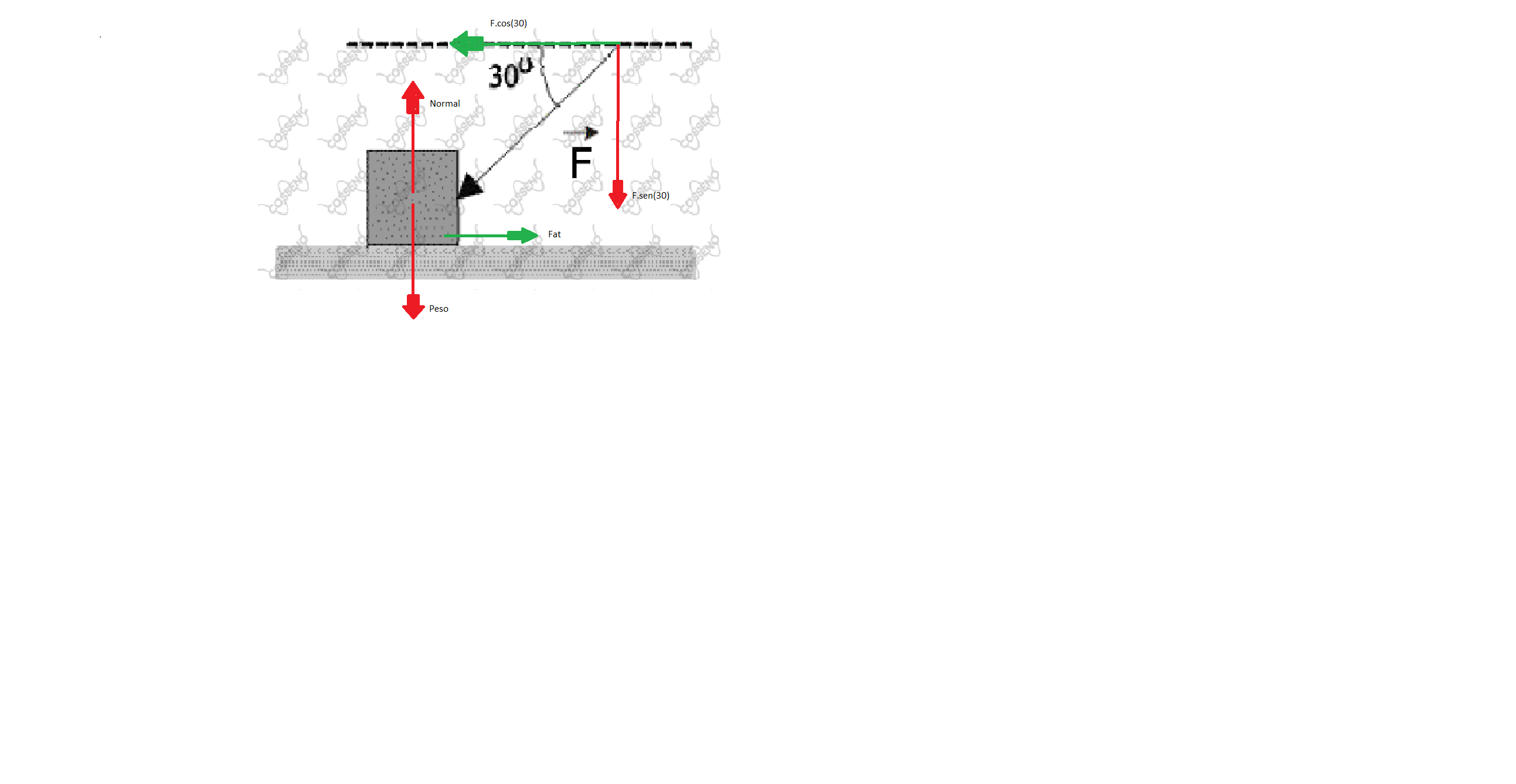
As forças horizontais que atuam sobre o bloco é a componente horizontal da força $F$ e a força de atrito $fat$ . Na iminência de movimento temos que $F \cos30° = fat = \mu N$ , onde $\mu$ é o coeficiente de atrito entre o bloco e o assoalho e $N$ é a normal que atua sobre o bloco.
As forças verticais que atuam sobre o bloco é a componente vertical da força $F$
, o seu peso $P$ e a normal $N$. Como o bloco não se move na vertical temos que $N = P + F \sin30°$
Com esses dados podemos escrever o seguinte sistema
$\begin{cases}
F \cos30° = \mu N\\
N = P + F \sin30°
\end{cases}$
$\implies F \cos30° = \mu(P + F \sin30°) = \dfrac{F \sqrt{3}}{2} = 0,25 \left(20 \cdot 10 + \dfrac{F}{2}\right)$
$ = \dfrac{F \sqrt{3}}{2} = 0,25 \left(200+ \dfrac{F}{2}\right)= \dfrac{F \sqrt{3}}{2} = \dfrac{F}{8} + 50$
$\implies F\left(\dfrac{4\sqrt{3}}{8} - \dfrac{1}{8}\right) = 50\implies F = \dfrac{400}{4\sqrt{3} - 1}$
$= \boxed{F \approx 68N}$
$\textbf{Resposta : Alternativa D}$


