As cargas positivas irão gerar um campo elétrico de afastamento e as cargas negativas irão criar um campo elétrico de aproximação $E_{1}=$ campo elétrico gerado pela $q_{1}$ $E_{2}=$ campo elétrico gerado pela $q_{2}$ $E_{3}=$ campo elétrico gerado pela $q_{3}$ $E_{4}=$ campo elétrico gerado pela $q_{4}$ 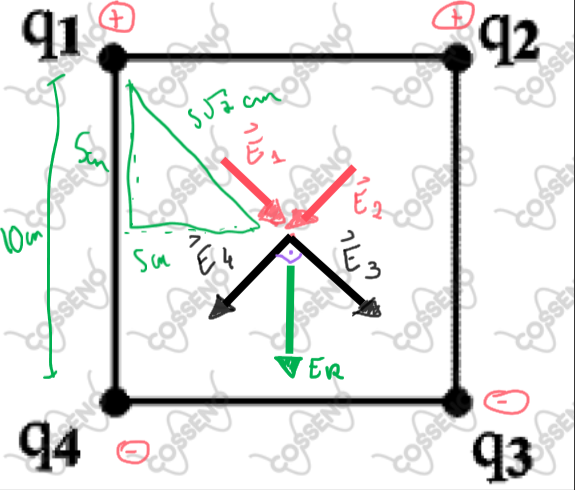Como as cargas possuem MÓDULOS iguais( $\left\vert{q}\right\vert=3 μC$ ) e estão à mesma distância do centro, os campos também possuirão MÓDULOS iguais: $\left\vert{E}\right\vert=\frac{K.q}{d^2}$ , aplicando geometria e trigonometria básica no quadrado, é fácil encontrar que $d=5\sqrt{2}cm$ $\left\vert{E}\right\vert=\frac{9.10^9.3.10^{-6}}{(5.\sqrt{2}.10^{-2})^2} = 54.10^{5}N/C$ 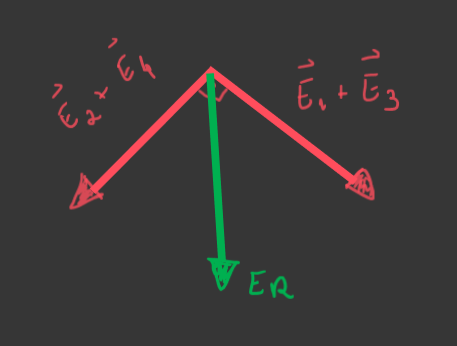$\left\vert{E_{1}}\right\vert+\left\vert{E_{3}}\right\vert=\left\vert{E_{2}}\right\vert+\left\vert{E_{4}}\right\vert=108.10^{5}N/C$ Como o ângulo entre os vetores resultante$=90^\circ$ $E_{r}=(108.10^{5}).\sqrt{2} N/C$ , considerando $\sqrt{2}=1,4$ $E_{r}=1,512.10^{7}N/C$ Alternativa c

O vetor campo elétrico $\vec{E_{1}}$ gerado pela carga $q_{1}$ sobre o centro do quadrado tem direção sudeste e sentido apontado para a carga $q_{3}$, o vetor campo elétrico $\vec{E_{2}}$ gerado pela carga $q_{2}$ sobre o centro do quadrado tem direção sudoeste e sentido apontado para a carga $q_{4}$ , o vetor campo elétrico $\vec{E_{3}}$ gerado pela carga $q_{3}$ sobre o centro do quadrado tem direção sudeste e sentido apontado para a própria carga geradora do campo $q_{3}$ , o vetor campo elétrico $\vec{E_{4}}$ gerado pela carga $q_{4}$ sobre o centro do quadrado tem direção sudoeste e sentido apontado para a própria carga geradora do campo $q_{4}$. Note que $E_{1} =E_{2} = E_{3} = E_{4} = E $ , porque o módulo das cargas são iguais($|q| = 3 \mu C$) e a distância do centro do quadrado à cargas são iguais. O vetor resultante na direção sudeste é igual a $E_{1} + E_{3} = 2E$ O vetor resultante na direção sudoeste é igual a $E_{2} + E_{4} = 2E$ Perceba que esses dois vetores formam entre si um ângulo igual a $90°$.O vetor campo elétrico resultante $E_{r}$ pode ser calculado por $E_{r}^2 = (2E)^2 + (2E)^2 \implies E_{r} = 2\sqrt{2} \cdot E$ , considere $k = 9\cdot 10^9 \text{ N.}\text{m}^2/\text{C}^2$ e $d$ a distância do centro do quadrado à cargas. $\therefore$ $E_{r} = 2\sqrt{2} \cdot E $ $= 2\cdot k \cdot \dfrac{|q|}{d^2} \cdot \sqrt{2} = 2\cdot 9 \cdot 10^9 \cdot \dfrac{3 \cdot 10^{-6}}{(5\sqrt{2} \cdot 10^{-2})^2} \cdot \sqrt{2}$ $= \dfrac{27}{25} \cdot 10^{7} \cdot \sqrt{2} = E_{r} \approx 1,08 \cdot 10^7 \cdot 1,41$ $\boxed{E_{r} \approx 1,53 \cdot 10^7 \text{ N}/\text{C}}$ $\textbf{Resposta : Alternativa C}$