Uma pessoa carrega em uma sacola as letras , , , , , e . Retirando-se cada letra aleatoriamente da sacola, sem reposição, a probabilidade de se formar as palavras e , nesta ordem, é:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

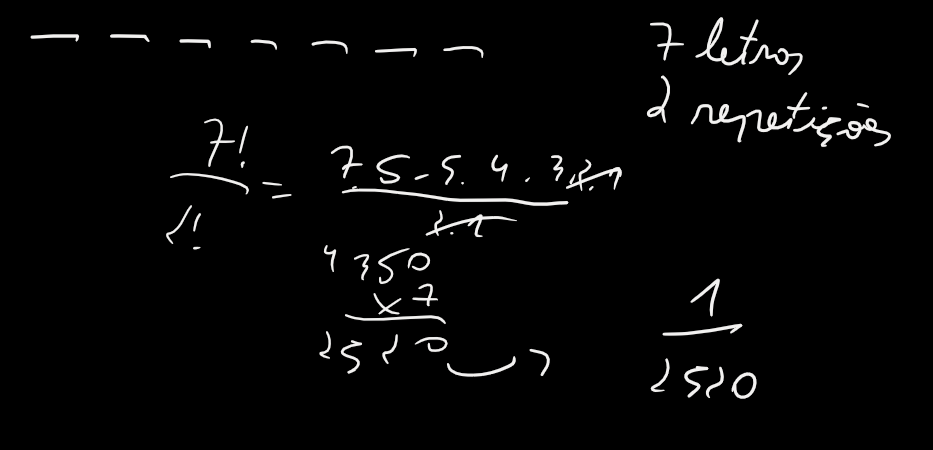
Ampliar Imagem
Basta determinar as probabilidades de cada decisão e, pelo Princípio Multiplicativo, multiplicar as probabilidades. O espaço amostral é de $7$ elementos.
A probabilidade de retirar $A$, no princípio, é de $\Large{\frac{2}{7}}$ .
A probabilidade de retirar $E$ corresponde a $\Large{\frac{1}{6}}$ .
A probabilidade de retirar $R$ corresponde a $\Large{\frac{1}{5}}$ .
A probabilidade de retirar $O$ corresponde a $\Large{\frac{1}{4}}$ .
A probabilidade de retirar $F$ corresponde a $\Large{\frac{1}{3}}$ .
A probabilidade de retirar $A$ corresponde a $\Large{\frac{1}{2}}$ .
A probabilidade de retirar $B$ corresponde a $1$ .
Temos que a probabilidade do evento $AERO$ e $FAB$ ocorrer é:
$\boxed{\frac{2}{7}\cdot \frac{1}{6}\cdot \frac{1}{5}\cdot \frac{1}{4}\cdot \frac{1}{3}\cdot \frac{1}{2}\cdot 1 = \frac{2}{7!} = \frac{1}{2520}}$ Alternativa $\mathbb{(B)}$


