Se é um arco do terceiro quadrante e , então vale:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

arcos no terceiro quadrante: $(\pi,\frac{3\pi}{2})$ $\implies$ $\sin x, \cos x < 0$
$\tg x=\frac{\sin x}{\cos x} = \frac{1}{3}$ $\implies$ $3\cdot \sin x = \cos x $
Elevando a igualdade ao quadrado:
$9\cdot \sin^{2} x=cos^{2} x$ $\implies$ $9\cdot \sin^{2} x + 9\cdot \cos^{2} x=10\cdot cos^{2} x$
$9\cdot \underbrace{(\sin^{2} x +\cos^{2} x)}_{1}=10\cdot cos^{2} x$ $\implies$ $\cos^{2} x = \frac{9}{10}$, $\cos x <0$, $\cos x = -\frac{3}{\sqrt {10}}$.
Como $3\cdot \sin x = \cos x $ $\implies$ $\sin x =-\frac{1}{\sqrt {10}}$.
Sabendo que $\sec x = \frac{1}{\cos x} = -\frac{\sqrt {10}}{3}$
Então $\sin x + \sec x = -\frac{1}{\sqrt {10}}-\frac{\sqrt {10}}{3}$ $=$ $-(\frac{\sqrt{10}}{10}+\frac{\sqrt {10}}{3})$ $=$ $-(\frac{3\sqrt{10}}{30}+\frac{10\sqrt {10}}{30})$
$\sin x + \sec x = \frac{-13\sqrt{10}}{30}$
Letra B (o gabarito aqui na plataforma esqueceu o sinal negativo nas alternativas)
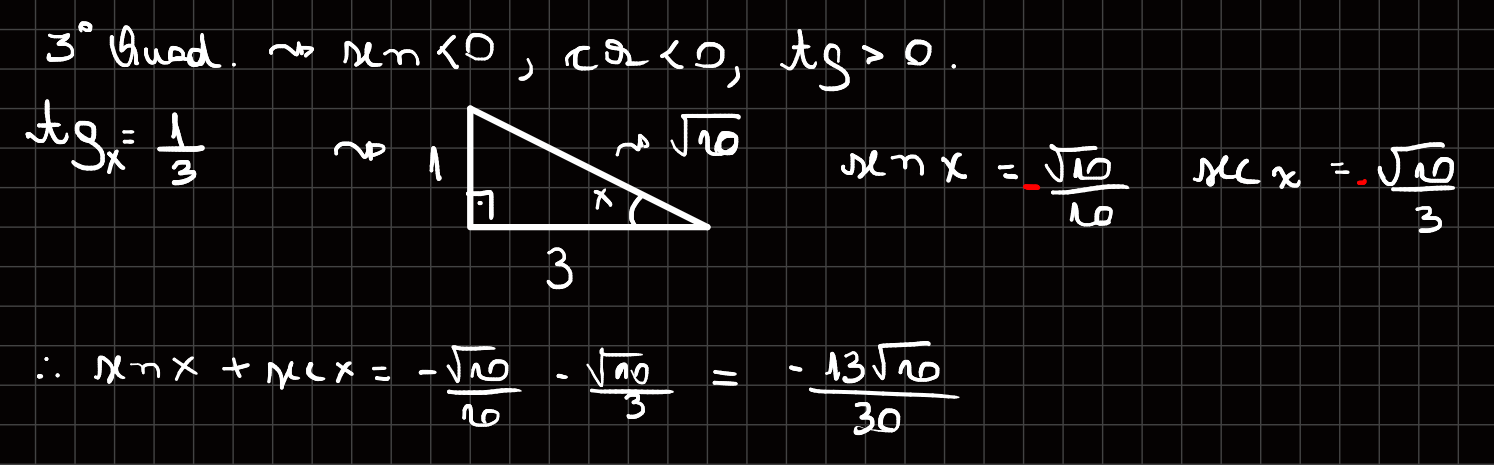
Ampliar Imagem


