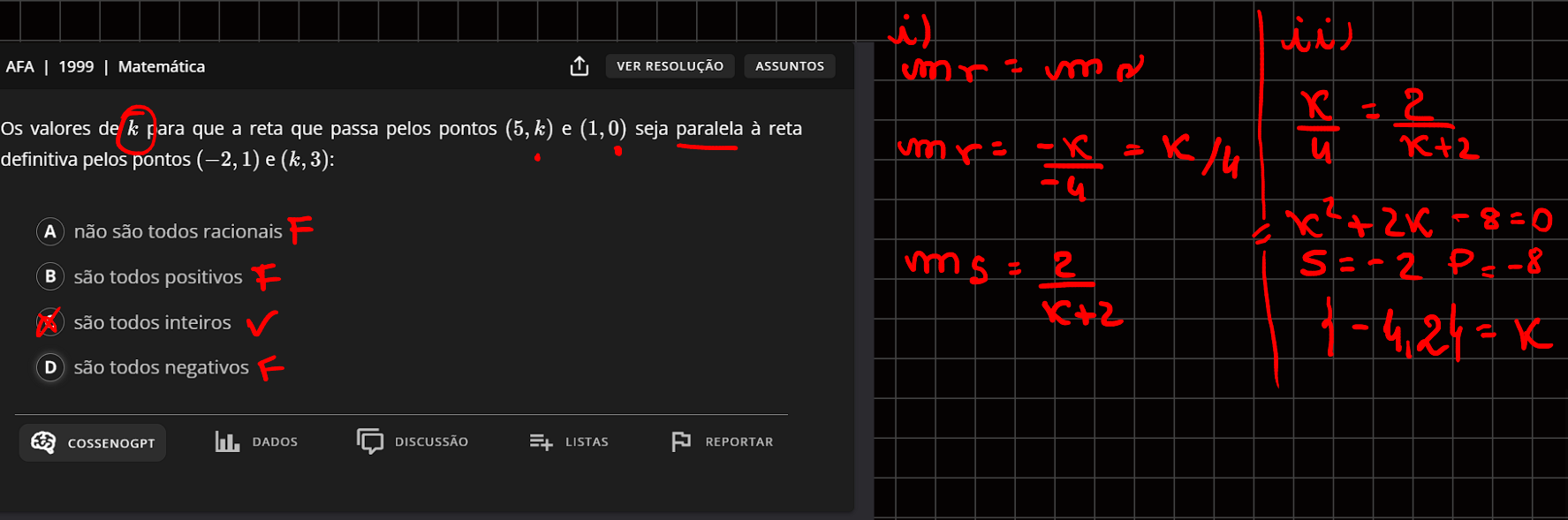
Os valores de para que a reta que passa pelos pontos e seja paralela à reta definitiva pelos pontos e :
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Toda reta pode ser escrita da forma $ \pu{ax + b = y} $ , em que "a" é o coeficiente angular, e "b" é o coeficiente linear da reta.
Portanto, tomando como base os pares de pontos dados, podemos descobrir os coeficientes angulares dele. E, como a questão pede os valores de K para os quais as retas sejam paralelas, seus coeficientes angulares devem ser iguais(condição de paralelismo: duas retas só são paralelas se seus coeficientes angulares forem iguais)
1) Pontos (-2,1) e (k,3):
$$ a_{1}x + b_{1} = y \therefore \begin{cases}
& \text{} -2a_{1} + b_{1} = 1 \\
& \text{} k.a_{1} + b_{1} = 3
\end{cases} \therefore a_{1} = \frac{2}{k+2} $$
O que fazemos nesse sistema foi apenas subtrair as equações, e isolar o $ \pu{a_{1}} $
2) Pontos (5,k) e (1,0):
$$ a_{2}x + b_{2} = y \therefore \begin{cases}
& \text{} 5a_{2} + b_{2} = k \\
& \text{} a_{2} + b_{2} = 0
\end{cases} \therefore a_{2} = \frac{k}{4} $$
Assim, podemos igualar $$ \pu{a_{1} = a_{2}} \therefore \frac{2}{k+2} = \frac{k}{4} \therefore k^2 + 2k - 8 = 0 \therefore \pu{k = 2 ou k = -4} $$
Gabarito, Letra C!
Vejam como é simples quando usamos DeltaY/DeltaX

Ampliar Imagem
A princípio, denominemos $A=(1,0)$ e $B=(5,k)$. Obtêm-se, nesse sentido, os vetores $\overrightarrow{AP}=(x-1, y)$, sendo $P=(x,y)$ um ponto genérico, e $\overrightarrow{AB}=(4,k)$.
Calculando o determinante: $\begin{vmatrix}
x-1 & y\\
4 & k
\end{vmatrix} = 0$ $\implies$ $r: k\cdot x -4\cdot y - k = 0$
Uma reta $s$, paralela a $r: k\cdot x -4\cdot y - k = 0$, tal que $r$ tenha vetor normal $n_r=(k,-4)$, tem como característica o mesmo vetor normal da paralela, logo:
$n_r=n_s=(k,-4)$. Isto significa que a reta $s$ é da forma $s: k\cdot x -4\cdot y +l = 0$.
Se $(−2,1)$ e $(k,3)$ passam por $s$, então encontra-se o sistema:
$\left\{ \begin{array}{rc}
-2\cdot k - 4 + l = 0\\
k^{2} - 12 + l = 0\\
\end{array}\right.$ $\implies$ $\left\{ \begin{array}{rc}
-2\cdot k - 4 + l = 0\\
k^{2} - 8 - 4 + l = 0\\
\end{array}\right.$ $\implies$ $k^{2}+2\cdot k - 8 = 0$
Completando quadrado, temos:
$k^{2}+2\cdot k +1$ = $8+1$ = $9$
$(k+1)^{2}$ = $9$ $\implies$ $|k+1|$ = $3$ $\implies$ $k = \{-4,2\}$
São todos inteiros.



