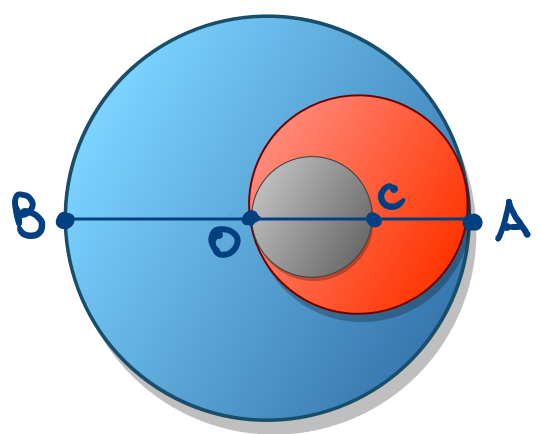
Sendo $OA = R$ o raio do círculo de centro "O", este sendo o maior círculo, temos que $OC = \dfrac{R}{2}$ é o raio do círculo de centro $C$, de modo que, o círculo que o tangencia interiormente é o menor círculo e o seu raio é a metade do círculo de centro $C$, ou seja, $\dfrac{R}{4}$. Portanto, a razão da área do maior círculo para a do menor vale:$$\boxed{\dfrac{\pi\cdot R^2}{\dfrac{\pi\cdot R^2}{16}}~=~16}$$$$\bf{Alternativa~(A)}$$

1