Analise a figura abaixo.
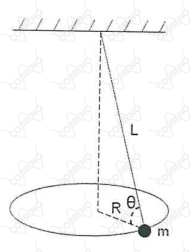
A figura mostra um pêndulo cônico no qual um pequeno objeto de massa m, preso à extremidade inferior de um fio, move-se em uma circunferência horizontal de raio R, com o módulo da velocidade constante. O fio tem comprimento L e massa desprezível. Sendo g a aceleração da gravidade e sabendo que a relação entre a tração T e o peso P do objeto é , qual o período do movimento?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Observa-se que $\cos \theta = \large{\frac{R}{L}}$.
Como a tração $T = 4mg$ não está contida nos eixos-padrão, a decompomos, de tal modo que:$$T\cdot \cos \theta = m\cdot w^2R \implies \frac{4gR}{L} = w^2R \implies \frac{4g}{L} = w^2$$
Sabe-se que $w = \large{\frac{2\pi}{\Tau}}$, sendo $\Tau \space$ o período do movimento, assim:$$\frac{4g}{L} = \left(\frac{2\pi}{\Tau} \right)^2 = \frac{4\pi^2}{\Tau ^2} \implies \boxed{\Tau = \left( \frac{\pi^2 L}{g} \right)^{\frac{1}{2}}}$$
$$\text{Alternativa } \mathbb{(D)}$$

