Analise a figura abaixo.
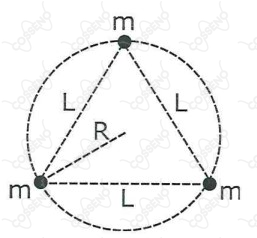
A figura acima mostra um sistema isolado de três partículas de massa m, ocupando os vértices de um triângulo equilátero inscrito em uma circunferência de raio R. Nessa configuração, a energia potencial gravitacional é . Considerando que a energia potencial gravitacional é nula no infinito, se o raio é reduzido à metade, qual é a razão entre variação da energia potencial gravitacional do sistema e a energia potencial gravitacional inicial, ?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Vamos trabalhar na geometria do problema.
Seja:
$$R=\frac{L\sqrt{3}}{4}$$
Energia potencial Gravitacional:
$$Uo=-\frac{Gm².\sqrt{3}}{4R}$$
$$\Delta U=-\frac{2Gm².\sqrt{3}}{4R}+\frac{Gm².\sqrt{3}}{4R}=-\frac{Gm².\sqrt{3}}{4R}$$
$$\frac{\Delta U}{Uo}=1$$

