Analise a figura abaixo.
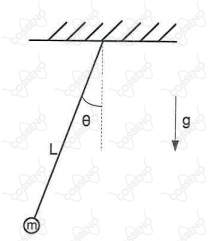
A figura acima mostra um pêndulo oscilando em movimento harmônico simples. Sua equação de posição angular em função do tempo é dada por: radianos. Sabe-se que é o comprimento do pêndulo, e é a aceleração da gravidade local. Qual a velocidade linear, em m/s, da massa , quando passa pelo ponto mais baixo de sua trajetória?
considere $\pi =3$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Análise da Dinâmica do problema.
$$mg=mw²L$$
$$w=\sqrt{\frac{10}{2,5}}=2$$
Derivando a equação da posição angular em relação ao tempo temos que:
$$w(t)=\frac{2.sen(2t)}{10}=\frac{1}{5}.sen(2t)$$
Como $v=wr$, para que $v$ seja máximo, $w$ precisa ser máximo também, logo $w=0,2$
$$v=0,5$$

