Analise a figura abaixo.
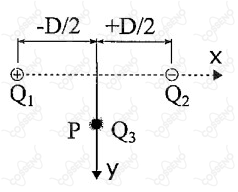
As cargas pontuais e estão equidistantes da carga , que também possui módulo igual a , mas seu sinal é desconhecido. A carga está fixada no ponto sobre o eixo , conforme indica a figura acima. Considerando e ( é a constante eletrostática), qual a expressão do módulo da força elétrica resultante em , em newtons, e em função de ?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Não importa o sinal do carga, a força resultante sobre $Q3$ será de $2F.cos \theta$, em que F é o módulo da força elétrica entre $Q1$, $Q2$ com $Q3$, e $\theta$ o ângulo $P\widehat{Q1}Q2$ do triângulo isóceles $PQ1Q2$.
$$cos\theta = \frac{D}{2\sqrt{y²+\frac{D²}{4}}}=\frac{1}{\sqrt{y²+1}}$$
$$F=\frac{4.k.qo²}{4y²+D²}=\frac{10}{y²+1}$$
Substituindo:
$$Res=2.\frac{10}{y²+1}.\frac{1}{\sqrt{y²+1}}$$
$$Res=\frac{20}{(y²+1)^\frac{3}{2}}$$

