Analise a figura abaixo.
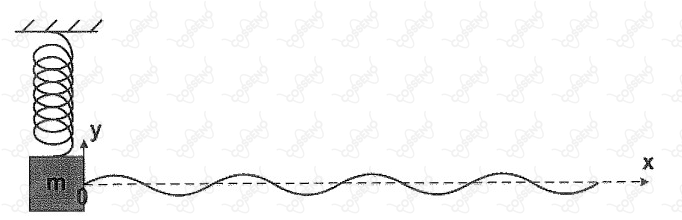
A figura acima mostra uma montagem em que o bloco de massa , preso à extremidade de uma mola vertical, oscila em torno da sua posição de equilíbrio. No bloco, prende-se uma corda muito longa estendida na horizontal. A massa específica linear da corda é . Após algum tempo, estabelece- se na corda uma onda transversal cuja equação é dada por , onde e estão em metros e em segundos. Nessas condições, a constante elástica da mola, em , e a tração na corda, em , são, respectivamente:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Olhando apenas para o cosseno da equação de onda, temos que:
$$cos(2x-30t)=cos(\frac{2.\pi.x}{\lambda}-\omega to+\phi)$$
$$\omega=30$$
$$K=\omega².m=900.0,7=630$$
Voltando para a equação temos que:
$$cos(2(x-15t))$$
$$\frac{1}{VT}=1$$
$$\frac{1}{T}=15$$
$$V=15$$
Com a velocidade de propagação, iremos agora utilizar a formula de Taylor para o cálculo da tração.
$$T=V².\mu=225.1,6.10^{-4}=36mN$$

