Analise a figura abaixo.
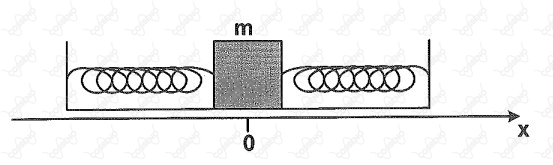
A figura acima mostra duas molas ideais idênticas presas a um bloco de massa e a dois suportes fixos. Esse bloco está apoiado sobre uma superfície horizontal sem atrito e oscila com amplitude em torno da posição de equilíbrio . Considere duas posições do bloco sobre o eixo e . Sendo e as respectivas velocidades do bloco nas posições e , a razão entre os módulos das velocidades, $\dfrac{v_1}{v_2} é
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Lembre que a energia mecânica para um MHS de UMA MOLA é dada pela expressão: $\frac{K.A²}{2}$. Como há a acão de duas molas em paralelo, devemos considerar que a energia mecânica desse sistema será de $K.A²$.
Conservando a energia mecânica nas duas situações temos:
$$KA²=\frac{m.v1²}{2}+\frac{2KA²}{16.2}$$
$$mv1²=\frac{15KA²}{8}$$
$$KA²=\frac{m.v2²}{2}+\frac{2.9KA²}{16.2}$$
$$mv2²=\frac{7.KA²}{8}$$
Dividindo uma pela outra, temos
$$\frac{v1}{v2}=\sqrt{\frac{15}{7}}$$

