Seja: $w=x+yi$ Logo: $z=-(2x+5y) +i(5x-2y)$ Calculando os módulos dos complexos que formam o triângulo: $$|z|²= (2x+5y)²+(5x-2y)²=29(x²+y²)$$ $$|w|²=x²+y²$$ $$|z-w|²=-(3x+5y)²+i(5x-3y)²=34(x²+y²)$$ Como podemos tratar Números complexos como vetores, apliquemos a Lei dos Cossenos no $\Delta AOB$: $$|z-w|²=|z|²+|w|²-2|z||w|cos\theta$$ $$cos\theta=\frac{|z|²+|w|²-|z-w|²}{2|z||w|}$$ $$cos\theta=\frac{29(x²+y²)+x²+y²-34(x²+y²)}{2\sqrt{29}\sqrt{x²+y²}\sqrt{x²+y²}}$$ $$cos\theta=\frac{-4}{2\sqrt{29}}$$ $$cos\theta=\frac{2\sqrt{29}}{29}$$

Seja$$z~=~a+bi \implies A=(a~,~b)\\w~=~c+di \implies B=(c~,~d)$$Do enunciado, temos$$z~=~-2(c+di)+5(ci-d)~=~(-2c-5d)+(5c-2d)i$$Logo $A = (-2c-5d~,~5c-2d)$. Assumindo o número complexo $w = 1+0i$, teremos os pontos $A = (-2~,~5)$ e $B = (1~,~0)$. O esquema no plano complexo segue-se abaixo: 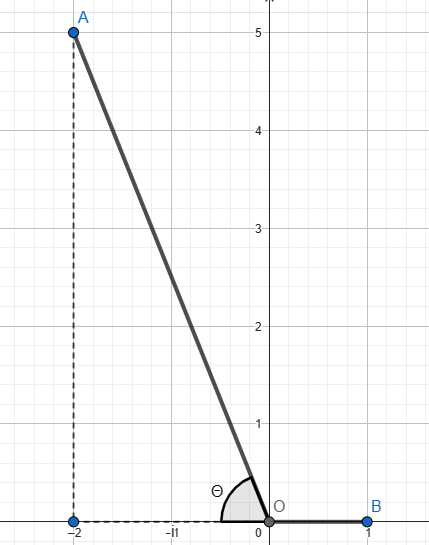Assim:$$cos~ \theta = \dfrac{-2}{\sqrt{5^2+2^2}}~=~-\dfrac{2\sqrt{29}}{29}$$Como $\angle AOB = 180°-\theta$, então $\boxed{\cos(AÔB) =-\cos \theta = \dfrac{2\sqrt{29}}{29}}$$$\bf{Alternativa~(C)}$$