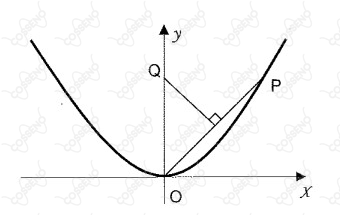
A figura abaixo mostra um ponto sobre a parábola e um ponto onde a mediatriz do segmento intercepta o eixo . A medida que tende à origem ao longo da parábola, o ponto tende para a posição limite
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A mediatriz de $OP$ possui coordenadas ($\frac{xp}{2},\frac{xp²}{2}$) sendo $xp$ a abcissa do ponto $P$.
Coeficiente angular de $OP$ é $mp=\frac{xp²}{xp}=xp$
Como a mediatriz é perpendicular a $OP$, com a condição de perpendicularidade, o coeficiente angular da reta mediatriz é: $m=-\frac{1}{xp}$.
Sendo $y$ a ordenada do ponto $Q$. Assim:
$$-\frac{1}{xp}=\frac{\frac{xp²}{2} -y}{\frac{xp}{2}}$$
$$y=\frac{xp²+1}{2}$$
Aplicando o limite na função $y$ temos:
$$\lim_{x \to 0}y=\lim_{x \to 0}\frac{xp²+1}{2}=\frac{1}{2}$$
Assim, $Q$ tende a ($0,\frac{1}{2}$).

